МЕХАНИКА. определение момента инерции твердых тел с помощью маятника максвелла
ЛАБОРАТОРНАЯ РАБОТА № 6
определение момента инерции твердых тел с помощью маятника максвелла
САНКТ-ПЕТЕРБУРГ 2011 г. Цель работы - изучение маятника Максвелла и определение с его помощью момента инерции твердых тел.
Общие сведения Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от распределения массы тела относительно оси вращения. Для вычисления момента инерции твердого тела относительно данной оси разобьем мысленно тело на большое число весьма малых элементов - материальных точек. Тогда момент инерции тела
или
где D mi - масса элемента; ri - расстояние от элемента до оси вращения; r - плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения. Таким образом, задача нахождения момента инерции сводится к интегрированию. В данной работе момент инерции определяется экспериментально с помощью маятника Максвелла.
Выведем расчетную формулу для момента инерции маятника на основе закона сохранения энергии. Когда маятник поднят на высоту h, его полная энергия состоит только из потенциальной энергии E п = mgh. В наинизшем положении маятника E п = 0, а полная энергия равна сумме кинетических энергий поступательного и вращательного движений:
Из закона сохранения энергии следует, что полная энергия маятника в верхнем и нижнем положениях должна быть одинакова, т.е.
Отсюда момент инерции
Поскольку поступательное движение маятника возникает только за счет вращательного, то угловая (w) и линейная (u) скорости связаны соотношением
Подставив уравнение (2) в (1), получим
Для равнопеременного движения связь между h, u и t может быть записана в виде
Подставив выражение для u в формулу (3), получим окончательно
Формулу (4) можно было бы вывести и на основе уравнений динамики для поступательного и вращательного движения.
Порядок выполнения работы
Общий вид установки представлен на рис.2. В основании 1 закреплена колонка 2, к которой прикреплен неподвижно верхний кронштейн 9 и подвижный нижний кронштейн 7. На верхнем кронштейне находится электромагнит 10 и фотоэлектрический датчик 11, а на нижнем кронштейне – фотоэлектронный датчик 3. Маятник представляет собой диск 5, закрепленный на оси 6, подвешенной на двух нитях 4 (бифилярный подвес). На диск можно насаживать сменные кольца 12, изменяя таким образом момент инерции системы. Маятник удерживается в верхнем положении электромагнитом 10. Фотоэлектрические датчики 3 и 11 соединены с электронным секундомером 2. Верхний электронный датчик задает момент начала движения маятника, а нижний - окончания движения (опускания) маятника. Последовательность проведения измерений следующая: 1) надеть на диск маятника одно из колец (если оно не надето); 2) намотать на ось маятника нить подвески до фиксации маятника в верхнем положении электромагнитом; 3) измерить время падения маятника по прибору; 4) повторить пп.1-3 еще пять-десять раз; 5) по указанию преподавателя провести измерения еще с другими кольцами; 6) по измеренным значениям времени определить среднее значение времени падения маятника
и по шкале на вертикальной колонке прибора длину маятника h. При обработке результатов эксперимента вычислить общую массу маятника
где R 0 - радиус оси маятника.
Теоретическое значение момента инерции маятника
где J 0 - момент инерции оси маятника,
J к - момент инерции кольца, надетого на диск, J д - момент инерции диска,
R д и R к - радиусы диска и кольца соответственно. Для полученного экспериментально значения момента инерции следует вычислить среднюю квадратичную погрешность
Записать окончательный результат в форме
Контрольные вопросы
1. Что такое момент инерции материальной точки? 2. Что такое момент инерции твердого тела? 3. От чего зависит величина момента инерции твердого тела? 4. Каков принцип действия маятника Максвелла? 5. Какие силы вызывают поступательное движение маятника? 6. Момент каких сил вызывает вращательное движение маятника? 7. Вывести формулу для определения момента nинерции с помощью маятника Максвелла.
МЕХАНИКА
ЛАБОРАТОРНАЯ РАБОТА № 7
измерение скорости полета пули с помощью баллистического маятника
САНКТ-ПЕТЕРБУРГ 2011 г.
Цель работы - определить скорость полета пули с помощью крутильных колебаний баллистического маятника.
Общие сведения
Скорость полета пули может достигать значительной величины, поэтому ее прямое измерение, т.е. определение времени, за которое пуля проходит известное расстояние, требует специальной аппаратуры. Разработаны и косвенные измерения скорости полета пули. Можно, например, использовать явление неупругого соударения.
На основании закона сохранения момента импульса можно написать
где m - масса пули; u - её скорость; l - расстояние от оси вращения маятника до точки удара пули; w - угловая скорость маятника; J - момент инерции маятника. Согласно закону сохранения механической энергии при повороте маятника кинетическая энергия маятника переходит в потенциальную энергию закручивающейся проволоки
где Из уравнений (1) и (2) можно получить
Так как момент инерции пули
Отсюда скорость пули
Модуль кручения проволоки D можно определить, измерив период крутильных колебаний маятника Т, так как при малых углах отклонения:
отсюда
Подставив выражение (6) в уравнение (4), найдем
Чтобы определить J, измерим периоды колебаний маятника Т 1 и Т 2 при различных положениях грузов R 1 и R 2:
отсюда:
Момент инерции маятника
где М - масса двух неподвижных грузов; R - расстояние от центра масс груза до оси вращения; J 0 - момент инерции маятника без грузов. Для различных положений грузов R1 и R2:
отсюда
Решая систему уравнений (9) и (10) найдем:
Запишем формулу (7) для положения грузов R1:
Подставив сюда формулу (11) получим окончательную формулу для расчета
Порядок выполнения работы
Общий вид баллистического маятника показан на рис.2. В основании 2, снабженном регулирующими ножками 1, позволяющими выравнивать прибор, закреплена колонка 3 с тремя кронштейнами: верхним 8, средним 4 и нижним 14. К кронштейну 4 прикреплено стреляющее устройство 9, прозрачный экран с нанесенной на него угловой шкалой 10 и фотоэлектрический датчик 12. Кронштейны 4 и 8 имеют зажимы, служащие для крепления стальной проволоки 13, на которой подвешен маятник, состоящий из двух мисочек 6, наполненных пластилином, двух перемещаемых грузов 7, двух стержней 5 и «водилки» 11. Фотоэлектрический датчик соединен разъемом с привинченным к основанию миллисекундомером.
Последовательность проведения опыта следующая: 1) установить максимальное расстояние между грузами; 2) выстрелить пулей из стреляющего устройства; 3) измерить максимальный угол отклонения amax маятника; 4) повторить пп. 2-3 три раза 5) отклонить маятник на угол amax и отпустить его; измерить время десяти колебаний и вычислить период Т 1; 6) установить минимальное расстояние между грузами; 7) отклонить маятник на угол amax и отпустить его; измерить время десяти колебаний и вычислить период Т 2; 8) по результатам эксперимента заполнить таблицу для n измерений (по указанию преподавателя):
Таблица 1
9) рассчитать скорость пули по формуле (13), (a– в радианах, М – масса одного груза; R – расстояние между центром масс груза и осью вращения). 10) рассчитать абсолютную погрешность D u. 11) записать результат для скорости пули
Контрольные вопросы
1. Что такое баллистический маятник? 2. От каких параметров установки зависит период колебаний баллистического маятника? 3. От чего зависит амплитуда колебаний баллистического маятника? 4. При каких упрощающих предположениях выведена формула (10)? 5. Можно ли пользоваться формулой (10), если удар пули о мишень происходит под углом, отличным от прямого?
|


 ,
, Маятник Максвелла представляет собой однородный диск С, через центр которого проходит металлический стержень D (рис.1). К концам этого стержня прикреплены две нити. Они тщательно, виток к витку, наматываются на стержень в направлении от его конца к диску. При освобождении маятника возникает поступательное движение вниз и вращательное вокруг оси симметрии. Вращение, продолжаясь по инерции в низшей точке движения (когда нити уже размотаны), приводит вновь к наматыванию нити на стержень, диск поднимается и движение снова повторяется, т.е. возникают колебания.
Маятник Максвелла представляет собой однородный диск С, через центр которого проходит металлический стержень D (рис.1). К концам этого стержня прикреплены две нити. Они тщательно, виток к витку, наматываются на стержень в направлении от его конца к диску. При освобождении маятника возникает поступательное движение вниз и вращательное вокруг оси симметрии. Вращение, продолжаясь по инерции в низшей точке движения (когда нити уже размотаны), приводит вновь к наматыванию нити на стержень, диск поднимается и движение снова повторяется, т.е. возникают колебания. .
. .
. (1)
(1) . (2)
. (2) . (3)
. (3) .
. . (4)
. (4)

 , где m 0 - масса оси; m д - масса диска; m к - масса кольца, и момент инерции маятника:
, где m 0 - масса оси; m д - масса диска; m к - масса кольца, и момент инерции маятника: ,
, ,
, ;
;

 .
. , сравнить экспериментальное значение J с теоретическим J т.
, сравнить экспериментальное значение J с теоретическим J т.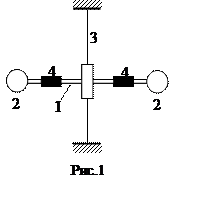 Если летящая пуля испытывает неупругий удар с неподвижным телом большей массы, их скорость после удара будет существенно меньше первоначальной скорости пули и ее можно будет измерить достаточно простыми методами, например, с помощью крутильных колебаний баллистического маятника, представляющего собой два стержня 1, подвешенных на вертикально натянутой проволоке 3 (рис.1). На стержнях закреплены мисочки с пластилином 2 и перемещаемые грузы 4. При попадании пули в мисочку с пластилином, маятник начинает поворачиваться вокруг своей вертикальной оси. Если пренебречь силами трения можно воспользоваться законами сохранения.
Если летящая пуля испытывает неупругий удар с неподвижным телом большей массы, их скорость после удара будет существенно меньше первоначальной скорости пули и ее можно будет измерить достаточно простыми методами, например, с помощью крутильных колебаний баллистического маятника, представляющего собой два стержня 1, подвешенных на вертикально натянутой проволоке 3 (рис.1). На стержнях закреплены мисочки с пластилином 2 и перемещаемые грузы 4. При попадании пули в мисочку с пластилином, маятник начинает поворачиваться вокруг своей вертикальной оси. Если пренебречь силами трения можно воспользоваться законами сохранения. , (1)
, (1) , (2)
, (2) - наибольший угол поворота маятника; D - модуль кручения проволоки.
- наибольший угол поворота маятника; D - модуль кручения проволоки. . (3)
. (3)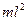 существенно меньше момента инерции маятника J, то выражение (3) можно записать в виде
существенно меньше момента инерции маятника J, то выражение (3) можно записать в виде
 . (4)
. (4) . (5)
. (5) (6)
(6) . (7)
. (7) . (8)
. (8)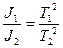 (9)
(9) ,
,

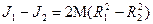 (10)
(10) (11)
(11) (12)
(12) . (13)
. (13)




