В робототехнике, есть две основные задачи кинематики:
прямая и обратная.
Рассмотрим эти задачи на стандартном примере манипулятора.
Прямая задача — это вычисление положения (X, Y, Z) рабочего органа манипулятора по его кинематической схеме и заданной ориентации (A1, A2… An) его звеньев (n — число степеней свободы манипулятора, A — углы поворота).
Обратная задача — это вычисление углов (A1, A2… An) по заданному положению (X, Y, Z) рабочего органа и опять же известной схеме его кинематики.
Т.о., решение прямой задачи говорит — где будет находиться рабочий орган манипулятора, при заданных углах его суставов, а обратная задача, наоборот, говорит: как нужно «вывернуться» манипулятору, чтобы его рабочий орган оказался в заданном положении.
Очевидно, что более распространённой и важной является именно обратная задача кинематики.
Но нужно иметь в виду, что эта задача редко может быть решена однозначно.
Дело в том, что хотя для углов (A1, A2,..., An) всегда существует ЕДИНСТВЕННОЕ положение (X, Y, Z) рабочего органа, но не факт, что для положения (X, Y, Z) отыщется такая же единственная комбинация углов (A1, A2,..., An).
Скорее всего, достичь заданного положения (X, Y, Z) возможно и при другой комбинации углов (A1', A2',..., An').
При решении обратной задачи аналитически, эта неоднозначность проявляется в явном виде (например, через квадратные корни).
Рассмотрим пример прямой задачи кинематики.

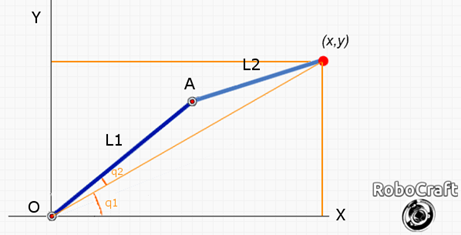
у нас есть манипулятор, способный работать только в одной плоскости и имеющий два сустава.
Первый сустав L1 закреплён на основании и повёрнут на угол Q1,
второй сустав L2, крепится к концу первого сустава и повёрнут относительно него на угол Q2.
Рабочий орган манипулятора находится на конце второго сустава.
Прямая задача кинематики состоит в нахождении координат рабочего органа (x, y) по заданным L1, L2, Q1, Q2.
L1 и L2 — это, соответственно, длины плеча и локтя манипулятора; определены конструкцией манипулятора.
Решение:
здесь, мы имеем две системы отсчёта — первая, связанная с точкой крепления плеча L1 — O, а вторая — с началом координат в точке крепления локтя — A.
Найдём смещение второй системы относительно первой (координаты точки A в системе отсчёта O):
XA = L1*cos(Q1)
YA = L1*sin(Q1)
Координаты (x, y) в системе отсчёта локтя:
x'' = L2*cos(Q2)
y'' = L2*sin(Q2)
По рисунку видно, что в системе O, локоть L2 повёрнут относительно плеча на Q1+Q2:
x' = L2*cos(Q1+Q2)
y' = L2*sin(Q1+Q2)
т.о.:
x = XA + x' = L1*cos(Q1) + L2*cos(Q1+Q2)
y = YA + y' = L1*sin(Q1) + L2*sin(Q1+Q2)
Теперь, рассмотрим пример обратной задачи кинематики.
тот же рисунок, но теперь нужно найти такие углы Q1 и Q2, которые позволят манипулятору с плечом L1 и локтем L2 поместить рабочий орган в заданную точку (x, y)

Проведём прямую B, соединяющую начало координат O с заданной точкой (x, y).
B^2 = x^2 + y^2
x = B*cos(q1)
y = B*sin(q1)
q1 — угол между осью OX и прямой B
q2 — угол между прямой B и плечом L1
отсюда:
Q1 = q1 - q2
q1 = arccos(x/B) или q1 = arctg(y/x)
, а q2 находим при помощи теоремы косинусов, которая говорит:
Для плоского треугольника со сторонами a,b,c и углом alpha, противолежащим стороне a, справедливо соотношение:
a^2 = b^2 + c^2 - 2*b*c*cos(alpha)
в нашем случае, по теореме косинусов:
L2^2 = B^2 + L1^2 - 2*B*L1*cos(q2)
=> q2 = arccos(L1^2 - L2^2 + B^2 / 2*B*L1)
Q1 = q1 - q2 = arccos(x/B) - arccos(L1^2 - L2^2 + B^2 / 2*B*L1)
по той же теореме косинусов найдём угол Q2:
как видно по рисунку, угол Q2 равен 180 — угол OAx
В^2 = L1^2 + L2^2 - 2*L1*L2*cos(PI - Q2)
Q2 = PI - arccos(L1^2 + L2^2 - B^2 / 2*L1*L2)
Очевидно, что руку можно расположить и по-другому:

формулы для Q1 и Q2 не изменятся, но изменятся знаки углов:
Q1 = q1 + q2
а Q2 нужно брать с противоположным знаком.
Откуда берётся изменение знака? Из вычисления квадратного корня, которое всегда даёт ответ со знаком плюс-минус.








