Статика
Статика Статика (от греч. statike — учение о весе, о равновесии), раздел механики, посвященный изучению условий равновесия материальных тел под действием сил. С. разделяют на геометрическую и аналитическую. В основе аналитической С. лежит возможных перемещении принцип, дающий общие условия равновесия любой механической системы. Геометрическая С. основывается на т. н. аксиомах С., выражающих свойства сил, действующих на материальную частицу и абсолютно твёрдое тело, т. е. тело, расстояния между точками которого всегда остаются неизменными. Основные аксиомы С. устанавливают, что: 1) две силы, действующие на материальную частицу, имеют равнодействующую, определяемую по правилу параллелограмма сил; 2) две силы, действующие на материальную частицу (или абсолютно твёрдое тело), уравновешиваются только тогда, когда они одинаковы по численной величине и направлены вдоль одной прямой в противоположные стороны; 3) прибавление или вычитание уравновешенных сил не изменяет действия данной системы на твёрдое тело. При этом уравновешенными называются силы, под действием которых свободное твёрдое тело может находиться в покое по отношению к инерциальной системе отсчёта. Методами геометрической С. изучается С. твёрдого тела. При этом рассматриваются решения следующих двух типов задач: 1) приведение систем сил, действующих на твёрдое тело, к простейшему виду; 2) определение условий равновесия сил, действующих на твёрдое тело. Необходимые и достаточные условия равновесия упруго деформируемых тел, а также жидкостей и газов рассматриваются соответственно в упругости теории, гидростатике и аэростатике. К основным понятиям С. относится понятие о силе, о моменте силы относительно центра и относительно оси и о паре сил. Сложение сил и их моментов относительно центра производится по правилу сложения векторов. Величина R, равная геометрической сумме всех сил Fk, действующих на данное тело, называется главным вектором этой системы сил, а величина М0, равная геометрической сумме моментов то (Рк) этих сил относительно центра О, называется главным моментом системы сил относительно указанного центра: R = Решение задачи приведения сил даёт следующий основной результат: любая система сил, действующих на абсолютно твёрдое тело, эквивалентна одной силе, равной главному вектору R системы и приложенной в произвольно выбранном центре О, и одной паре сил с моментом, равным главному моменту M0 системы относительно этого центра. Отсюда следует, что любую систему действующих на твёрдое тело сил можно задать её главным вектором и главным моментом. Этим результатом широко пользуются на практике, когда задают, например, аэродинамические силы, действующие на самолёт или ракету, усилия в сечении балки и др. Простейший вид, к которому можно привести данную систему сил, зависит от значений R и M0. Если R = 0, а M0 ¹ 0, то данная система сил заменяется одной парой с моментом M0. Если же R ¹ 0, а M0 = 0 или M0 ¹ 0, но векторы R и M 0 взаимно перпендикулярны (что, например, всегда имеет место для параллельных сил или сил, лежащих на одной плоскости), то система сил приводится к равнодействующей, равной r. Наконец, когда R ¹ 0, M0 ¹ 0 и эти векторы не взаимно перпендикулярны, система сил заменяется совокупным действием силы и пары (или двумя скрещивающимися силами) и равнодействующей не имеет. Для равновесия любой системы сил, действующих на твёрдое тело, необходимо и достаточно обращение величины R и M0 в нуль. Вытекающие отсюда уравнения, которым должны удовлетворять действующие на тело силы при равновесии, см. в ст. Равновесие механической системы. Равновесие системы тел изучают, составляя уравнения равновесия для каждого тела в отдельности и учитывая закон равенства действия и противодействия. Если общее число реакций связей окажется больше числа уравнений, содержащих эти реакции, то соответствующая система тел является статически неопределимой; для изучения её равновесия надо учесть деформации тел. Графические методы решения задач С. основываются на построении многоугольника сил и верёвочного многоугольника.
Силой называется физическая величина, являющаяся мерой механического взаимодействия тел. Сила – величина векторная. Она характеризуется величиной (модулем), направлением и точкой приложения. Основной единицей измерения силы является Ньютон [Н]. Совокупность сил, приложенных к телу, называется системой сил. Если все силы лежат в одной плоскости, то такая система сил называется плоской. Если силы не лежат в одной плоскости, то они образуют пространственную систему сил. Тело, которое из данного положения может переместиться в любое положение в пространстве, называется свободным телом. Две системы сил называют эквивалентными одна другой, если каждая из них, действуя по отдельности, может сообщить покоящемуся телу одно и то же движение Система сил, под действием которой покоящееся тело не изменяет своего состояния покоя, называется уравновешенной или эквивалентной нулю – Сила, которая одна заменяет действие системы сил на твёрдое тело, называется равнодействующей – Силы могут быть сосредоточенные (рис. 1.1, а) и распределенные (рис. 1.1, б). Сила, приложенная к какой-нибудь одной точке тела, называется сосредоточенной. Система распределенных сил характеризуется интенсивностью q, т.е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в Ньютонах, деленных на метры (Н/м).
а
б
Рис. 1.1
Распределенную нагрузку в виде прямоугольника (равномерно распределенная нагрузка) или треугольника заменяют одной силой (равнодействующей), которую прикладывают в центре тяжести площади распределения (рис. 1.1, б). Величина равнодействующей численно равна площади фигуры, образованной распределенной нагрузкой:
Аксиома 1. Если на свободное абсолютно твёрдое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по величине и направлены вдоль одной прямой в противоположные стороны (рис.1.2).
Рис.1.2
Аксиома 2. Действие данной системы сил на абсолютно твёрдое тело не изменится, если к ней прибавить или от неё отнять уравновешенную систему сил. Если Следствие: действие силы на абсолютно твёрдое тело не изменится, если перенести точку приложения силы вдоль её линии действия в любую другую точку тела. Пусть на тело действует приложенная в точке А сила
Рис.1.3
Аксиома 3. Две силы, приложенные к твёрдому телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах как на сторонах. Вектор
Рис.1.4
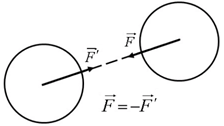
Аксиома 4. Закон равенства действия и противодействия. При всяком действии одного тела на другое имеет место такое же по величине, но противоположное по направлению противодействие (рис.1.5).
Рис.1.5
Аксиома 5. Принцип отвердевания. Равновесие изменяемого (деформируемого) тела, находящегося под действи-ем данной системы сил, не нарушится, если тело считать отвердевшим, т.е. абсолютно твёрдым.

Рис. 1.13
Это условие равновесия не является достаточным, т.к. равнодействующая этих сил может оказаться не равной нулю. Достаточным условием является наличие замкнутого силового треугольника при одновременном пересечения линий действия трех сил в одной точке. Рассмотрим тело, на которое действуют три непараллельные силы
Рис. 1.14
Так как эти силы непараллельны, то две любые силы, например, Следовательно, теперь на тело действуют только две силы
Главный вектор системы сил – величина, равная геометрической сумме сил системы. Главный вектор системы сил не следует путать с равнодействующей. Равнодействующая – всегда главный вектор, а главный вектор равен равнодействующей, если система сил является сходящейся. Равнодействующую плоской системы сходящихся сил можно определить графически и графоаналитически. Сложение двух сил. При графическом определении равнодействующей на чертеже и выбранном масштабе изображаются силы, затем они складываются по правилу параллелограмма. По длине диагонали параллелограмма, учитывая выбранный масштаб, определяется равнодействующая, равная сумме слагаемых сил. Точность определения равнодействующей зависит в этом случае от точности построения силового треугольника. Графоаналитический способ сложения сил позволяет более точно определить равнодействующую, используя тригонометрические зависимости: - теорему косинусов:
или - теорему синусов:
Рис. 1.6
Сложение трех сил, не лежащих в одной плоскости: геометрическую сумму
Рис. 1.7
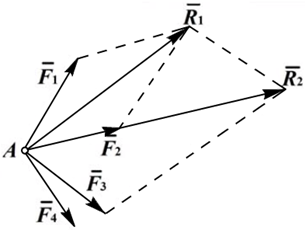
Сложение системы сил. Сложение плоской системы сходящихся сил осуществляется либо путём последовательного сложения сил с построением промежуточной равнодействующей (рис. 1.8), либо путём построения силового многоугольника (рис. 1.9).
Рис. 1.8
Рис. 1.9
1.4.2. Разложение сил
Разложить данную силу на составляющие – означает найти такую систему сил, для которой данная сила является равнодействующей. Подобная задача имеет однозначное решение, если необходимо разложить силу по двум направлениям, лежащим в одной плоскости. На рис. 1.10 показано разложение силы F по двум направлениям ab и cd.
Рис. 1.10
1) Геометрическое условие равновесия сходящейся системы сил: для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут (конец вектора последней слагаемой силы должен совместиться с началом вектора первой слагаемой силы). Тогда главный вектор системы сил будет равен нулю ( 2) Аналитические условия равновесия. Модуль главного вектора системы сил определяется по формуле
Rx = 0, Ry = 0, Rz = 0.
Следовательно, для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трёх координат осей были равны нулю:
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил на каждую из двух координатных осей были равны нулю:
Чтобы не вращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.
При приведении этой системы сил к произвольному центру (точке) О получим главный вектор R, приложенный в точке О, и пару сил с моментом Mo.
Главный вектор R системы параллельных сил параллелен силам, его модуль равен абсолютному значению алгебраической суммы проекций сил на ось (О1у), параллельную силам, а его направление определяется знаком этой суммы:
| R | = | Ry | = |S±Fk |. (k = 1, 2,..., n)
Момент пары сил Mo равен главному моменту параллельных сил F1, F2,..., Fn относительно центра приведения О:
Mo = S mo(Fk). (k = 1, 2,..., n)
Условия равновесия для плоской системы параллельных сил имеют вид:
R = 0, Mo = 0.
Из них следуют две формы аналитических условий равновесия для системы параллельных сил на плоскости.
1. Основная форма условий равновесия.
S Fky = S±Fky = 0, S mo(Fk) = 0. (k = 1, 2,..., n)
для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы сумма проекций сил на ось, параллельную силам, и сумма их моментов относительно точки, лежащей на плоскости действия сил, были равны нулю.
2. Вторая форма условий равновесия:
S mА(Fk) = 0, S mВ(Fk) = 0. (k = 1, 2,..., n)
Расстояние l между линиями действия сил пары называется плечом П. с. Действие, оказываемое П. с. на твёрдое тело, характеризуется её моментом, который изображается вектором М, равным по абсолютной величине Pl и направленным перпендикулярно к плоскости действия П. с. в ту сторону, откуда поворот, совершаемый П. с., виден происходящим против хода часовой стрелки (в правой системе координат). Основное свойство П. с.: действие, оказываемое ею на данное твёрдое тело, не изменяется, если П. с. переносить куда угодно в плоскости пары или в плоскости, ей параллельной, а также если изменить абсолютную величину сил пары и длину её плеча, сохраняя неизменным момент П. с. Таким образом, момент П. с. можно считать приложенным к любой точке тела.
Рычаг используется для получения большего усилия на коротком плече с помощью меньшего усилия на длинном плече (или для получения большего перемещения на длинном плече с помощью меньшего перемещения на коротком плече). Сделав плечо рычага достаточно длинным, теоретически, можно развить любое усилие.
Правило рычага лежит в основе принципа действия рычажных весов. Равновесие на таких весах достигается когда моменты сил, приложенные к обеим плечам рычага весов, оказываются одинаковыми. Момент силы — это произведение величины силы (в данном примере — это силы тяжести грузиков) на плечо силы, которое определяется как минимальное расстояние от центра вращения до линии действия силы.
В случае, когда достигается равновесие, также имеет место равенство нулю векторной суммы всех сил. Таким образом, сила реакции опоры в точке вращения равна по модулю сумме обеих сил тяжести:
| N | = | m1g + m2g |
Представленная модель позволяет варьировать: положение точки опоры; плечи обеих сил тяжести; массы подвешиваемых грузиков. Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Существуют три формы уравнений равновесия плоской системы сил. Первую форму получим, спроектировав на оси координат векторное равенство
Первые два уравнения называются уравнениями проекций сил на оси координат, третье - уравнением моментов. Точка
Легко доказать, что необходимые и достаточные условия равновесия плоской системы сил могут быть записаны еще в двух формах.
Вторая форма:
где ось проекций
Третья форма:
где точки
Отметим, что для любой из трех форм уравнений равновесия число независимых между собой уравнений равновесия равно трем. Задачи, в которых все неизвестные могут быть определены из уравнений равновесия твердого тела, называются статически определенными. Если же неизвестных больше, чем этих уравнений, то задача оказывается статически неопределенной.
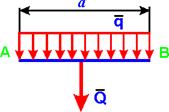 определенному закону. определенному закону.
1. Простейшим примером распределенных сил, лежащих в одной плоскости является равномерно-распределенная нагрузка. Такая система распределенных сил характеризуется постоянной по величине интенсивностью q - т. е. значением силы, приходящейся на единицу длины нагруженного участка. Размерность распределенной нагрузки [q] = H/м. При статических расчетах эту систему параллельных сил можно заменить равнодействующей Q, приложенной в середине отрезка АВ, а ее модуль равен Q = q× a.
Q = 0,5×q m × a. Линия действия этой силы проходит через центр тяжести треугольника, т. е. на расстоянии a /3 от основания ВС треугольника АВС.
|

 ,
,  .
. .
. .
. .
.

 .
.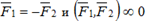

 , то
, то  .
. . Выберем на линии действия этой силы произвольную точку В, и приложим к ней уравновешенные силы
. Выберем на линии действия этой силы произвольную точку В, и приложим к ней уравновешенные силы  и
и  , причём
, причём  ,
,  . Так как силы
. Так как силы 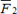 и
и  , равная
, равная  , но приложенная в точке В (рис.1.3).
, но приложенная в точке В (рис.1.3). 
 , равный диагонали параллелограмма, построенного на векторах
, равный диагонали параллелограмма, построенного на векторах  и
и 

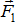 ,
,  и
и  (рис. 1.14).
(рис. 1.14).
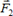 должны пересечься в некоторой точке А. Перенесём силы
должны пересечься в некоторой точке А. Перенесём силы  и
и  вдоль линии их действия и приложим их к точке А. Заменим сходящиеся силы
вдоль линии их действия и приложим их к точке А. Заменим сходящиеся силы  .
.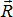 и
и  . Поскольку тело находится в равновесии под действием двух сил, то согласно первой аксиоме статики, эти силы должны действовать вдоль одной прямой АВ. Таким образом, линия действия силы
. Поскольку тело находится в равновесии под действием двух сил, то согласно первой аксиоме статики, эти силы должны действовать вдоль одной прямой АВ. Таким образом, линия действия силы 
 (рис.1.6);
(рис.1.6);




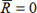 ).
). . Поскольку
. Поскольку  , то подкоренное выражение может быть равно нулю только в том случае, если каждое слагаемое одновременно обращается в нуль, т.е.
, то подкоренное выражение может быть равно нулю только в том случае, если каждое слагаемое одновременно обращается в нуль, т.е.



 и присоединив к получившимся двум уравнениям равенство
и присоединив к получившимся двум уравнениям равенство  , выражающее условие равенства нулю главного момента:
, выражающее условие равенства нулю главного момента: ,
,  ,
,  . (1.6)
. (1.6)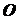 может быть выбрана произвольно.
может быть выбрана произвольно. ,
,  ,
, 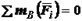 , (1.7)
, (1.7) должна быть не перпендикулярна к отрезку
должна быть не перпендикулярна к отрезку  .
. ,
,  ,
,  , (1.8)
, (1.8) не должны лежать на одной прямой.
не должны лежать на одной прямой. 2. Силы, распределенные вдоль отрезка по линейному закону. Для этих сил интенсивность q является переменной величиной, изменяющейся от нуля до максимального значения qm. равнодействующая Q таких сил по модулю равна площади треугольника АВС,
2. Силы, распределенные вдоль отрезка по линейному закону. Для этих сил интенсивность q является переменной величиной, изменяющейся от нуля до максимального значения qm. равнодействующая Q таких сил по модулю равна площади треугольника АВС,


