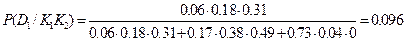Теоретическая часть. Метод Байеса является одним из наиболее простых и мощных методов
Метод Байеса является одним из наиболее простых и мощных методов. Этот метод основан на вычислении условной вероятности появления такого события как диагноз Di при появлении конкретной реализации комплекса признаков К* [1,2]. Рассмотрим первоначально основные положения этого метода на простейшем случае, когда имеется диагноз Di и один бинарный признак Кj, встречающийся при появлении этого диагноза. Определим некоторые понятия 1. P(Di) - априорная (до опытная) вероятность появления диагноза Di. Эту вероятность определяют по статистическим данным на начальном этапе применения метода исходя из следующих соображений. Если при обследовании N объектов диагноза установлено, что из них Ni имеют диагноз Di, то вероятность появления этого диагноза определяется соотношением
2. Р(Кj/Di) - априорная условная вероятность появления признака Кj у объектов имеющих техническое состояние (диагноз) Di. Эта вероятность так же определяется на начальном этапе по имеющимся статистическим данным. Если из N обследованных объектов Ni находилось в диагнозе Di, а из них Nij объектов имели признак Kj, то условная вероятность появления признака Кj у объектов с диагнозом Di вычисляется следующим образом
3. P(Kj) - априорная вероятность появления признака Kj у всех объектов независимо от их состояния. То есть, если из N объектов независимо от их технического состояния у Nj был обнаружен признак Kj, то эта вероятность определяется следующим соотношением
Напомним некоторые положения теории вероятностей. Пусть мы имеем два события А и В. Известны вероятности появления этих событий Р(А) и Р(В), а также условная вероятность появления события А при уже состоявшемся событии В Р(А/В) и условная вероятность появления события В при уже состоявшемся событии А Р(В/А). Тогда вероятность одновременного появления событий А и В Р(А,В) определяется следующей формулой
Р(А,В) = Р(А) Р(В/А) = Р(В) Р(А/В).
Воспользовавшись этой формулой и данными выше понятиями можно записать вероятность одновременного появления диагноза Di и признака Kj следующим образом
P(Di,Kj)=P(Di) P(Kj/Di)=P(Kj) P(Di/Kj).
В этом выражении величина P(Di/Кj) - это условная вероятность существования диагноза Di при обнаружении признака Kj, то есть это та величина, которая ищется при вероятностном подходе к решению задачи распознавания диагнозов. После соответствующих преобразований из последнего выражения получим формулу Байеса
P(Di/Kj)={P(Di) P(Kj/Di)}/ P(Kj). (1) Формула (1) получена для случая, когда при постановке диагноза используется один простой признак. Для принятия решения о диагнозе при использовании набора (комплекса) признаков применяется обобщенная формула Байеса, которую можно получить из следующих соображений. Если диагностирование проводится по комплексу признаков, то в результате обследования мы получаем конкретную реализацию каждого j-того признака Kj* и, следовательно, конкретную реализацию комплекса признаков К* в целом. В этом случае формула Байеса предстанет в виде:
где P(Di/К*) - условная вероятность нахождения объекта диагностики в диагнозе Di при условии, что в ходе обследования была получена реализация К* комплекса признаков К; Р(К*) -вероятность появления конкретной реализации К* комплекса признаков К у всех диагностируемых объектов, независимо от их технического состояния; Р(К*/Di) - условная вероятность появления конкретной реализации К* комплекса диагностических признаков К для объектов, находящихся в диагнозе Di.
Преобразуем последние выражения с учетом следующих соображений. Примем, что система может находится только в одном из n технических состояний, тогда
Будем считать, что отдельные диагностические признаки, входящие в состав комплекса признаков, независимые. Такое допущение вполне справедливо для реальных условий при большом числе влияющих факторов. Тогда условную вероятность Р(К*/Di) в соответствии с известными положениями теории вероятностей можно представить как произведение
где P(K*j/Di) - условная вероятность появления конкретной реализации К*j j-того признака при нахождении объекта диагностики в диагнозе Di; j= 1... l. Вероятность же появления конкретной реализации комплекса признаков при нахождении объекта во всех диагнозах Р(К*) можно представить следующим образом
С учетом последних соотношений уравнение (2) перепишем в окончательном виде
Полученное уравнение называется обобщённой формулой Байеса. В большинстве практических задач, особенно при большом числе признаков, можно принимать условие независимости признаков даже при наличии существенных корреляционных связей между ними и тогда
Для определения вероятности диагноза по методу Байеса составляется исходная диагностическая матрица (табл. 1.1), которая формируется на основе предварительного статистического материала. В этой таблице содержатся вероятности разрядов признаков P(Kjs/Di) при различных диагнозах. Если признаки двухразрядные (простые признаки "да-нет"). то в табл. 1.1 достаточно указать вероятность появления признака P(Kj/Di). Вероятность отсутствия признака
Сумма вероятностей всехреализаций признака Кjравна единице
При методе Байеса используется следующее правило: объект с комплексом признаков К* относится к диагнозу (классу) с наибольшей вероятностью К *Î;Di, если P(Di/K*)>P(Dj/K*), j=1, 2, … l; i¹j.
Таблица 1.1 Диагностическая матрица
Пример При диагностировании степени электрокоррозии арматуры железобетонных опор с помощью прибора АДО-2М проверяются два признака: K1 – заниженное значение потенциала арматуры и К2- завышенное значение декремента колебаний опоры. Появление этих признаков связано либо с образованием трещин в опоре (состояние D1), либо наличием коррозии в арматуре опоры (состояние D2). При нормальном состоянии опоры (состояние D3) признак К1 не наблюдается, а признак К2 наблюдается в 4% случаях. В состоянии D2 признак K1 встречается в 18%, а признак К2 -в 31% случаев. В состоянии D2 признак K1 встречается в 38%, а признак К2-в 49% случаях. Известно, что по окончанию срока службы 73% опор имеют нормальное состоянии, 6% опор имеют состояние D1 и 17% - состояние D2. Требуется определить состояние опоры (поставить диагноз) при возможных сочетаниях проверяемых признаков. 1. Сведем исходные данные в диагностическую таблицу (табл. 1.2). При этом вероятности отсутствия признаков
Таблица 1.2 Вероятности признаков и априорные вероятности состояний
2. Найдём вероятности, когда обнаружены оба признака P(Di/K1K2). Считая признаки независимыми, применим формулы (3) и (4). Вероятность состояния D1 при наличии признаков К1 и К2:
Аналогично получим P(D2/K1K2)=0.904; P(D3/K1K2)=0. 3. Определим вероятности нахождения опоры в различных состояний, если обследование показало, что потенциал в норме (признак К1 отсутствует), но увеличен декремент колебаний (признак К2 наблюдается). Используем те же формулы (3) и (4):
Аналогично получим P(D2/ 4. Вычислим вероятности состояний, когда признак К1 наблюдается, а признак К2 – отсутствует (формулы 3 и 4)
Соответственно P(D2/K1 5. Для случая, когда не наблюдаются оба признака:
P(D1/
Сведём результаты в табл. 1.3. Таблица 1.3 Результаты диагноза
5. Анализ приведённых результатов позволяет установить: - При наличии признаков К1 и К2 опора с вероятностью 0,90 имеется состояние D2 (повышенная коррозия арматуры). - При отсутствии обоих признаков наиболее вероятно нормальное состояние (вероятность 0,89). - При наблюдении только признака К1 наиболее вероятно состояние D2 . - При наблюдении только признака К2 однозначно дать ответ о техническом состоянии опоры нельзя, требуется проведение дополнительного обследования, т.к. связь признака с состояниями опоры выражена нечётко.
|

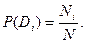
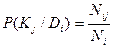

 (2)
(2)

 .
. (3)
(3) (4)
(4) (5)
(5) .
. вычислим по формуле (5).
вычислим по формуле (5). /Di)
/Di)
 /Di)
/Di)