Пример 1. Дана система трех линейных уравнений с тремя неизвестнымиДана система трех линейных уравнений с тремя неизвестными. Доказать ее совместност ь и решить тремя способами: 1) с помощью формул Крамера; 2) методом матричного исчисления; 3) методом Гаусса.
1 ) x1 - 5х2 + 2х3 = 6 3x1 - х2 - х3 = - 3 - 2 x1 + 2х2 + 3х3 = 3 Решение. Вычислим определитель системы. ∆= Так как ∆≠0, то система совместна и имеет единственное решение. Найдем ∆1, ∆2,∆3, - определители третьего порядка, полученные из определителя системы ∆ заменой 1, 2 и 3-го столбца соответственно столбцом свободных членов. ∆1 = Подставляя найденные значения определителей в формулы Крамера, получаем искомое решение системы: х1=∆1/∆=-1, х2= ∆2/∆=-1, х3= ∆3/∆= 1. Сделаем проверку. -1 - 5∙ (-1) + 2∙1 = 6 - верно, 3∙(-1) – (-1) – 1 = -3 - верно, -2∙(-1) + 2∙(-1) + 3∙1 = 3 - верно. Ответ: х1=-1, х2= -1, х3= 1. 2) Решим систему методом Гаусса.
x1 - 5х2 + 2х3 = 6 3x1 - х2 - х3= - 3 - 2 x1 + 2х2 + 3х3 = 3 Расширенная матрица системы имеет вид Шаг 1. 1-ю строку умножая на (- 3), 2 и прибавляя полученные строки соответственно ко второй, третьей строкам, исключим переменную x1 из второй и третьей строк. Шаг 2. 2-ю строку умножая на 4 и прибавяя к 3-ей, исключим из нее переменную х2. Таким образом, имеем:
Используя обратный ход метода Гаусса найдем из 3-го уравнения: 3х3 = 3 из 2 -го уравнения: 2х2 - х3 = -3 из 1 -го уравнения: x1 - 5х2 + 2х3 = 6 Ответ: х1=-1, х2= -1, х3= 1. 3). Решим систему уравнений матричным методом. Здесь
A = Так как определитель матрицы системы отличен от нуля: | A| = 42, то матрица А имеет обратную. Для нахождения обратной матрицы А-1 вычислим алгебраические дополнения элементов матрицы А и составим матрицу из алгебраических дополнений ||Ai j|| = Умножив слева обратную матрицу на матрицу столбец свободных членов, получим искомую матрицу столбец неизвестных: Х=А-1∙В или Х = Ответ: х1=-1, х2= -1, х3= 1. Пример 2. Даны вершины А1(3; -2; 2), А2(1; -3; 1), А3(2; 0; 4),А4(6; -4: 6). Средствами векторной алгебры найти: 1) длину ребра А1 А2 2) угол между ребрами А1 А2 и А1 А3 3) площадь грани А1А2А3 4) объем пирамиды А1А2А3А4 Решение. 1) Находим вектор А1А2:
Длину вектора, т.е. длину ребра А1А2 найдем по формуле
2) Найдем координаты вектора Скалярное произведение векторов
Отсюда следует, что φ; – тупой угол, φ;=π – arccos0,27 = 1,85 рад с точностью до 0,01. Это и есть искомый угол между ребрами А1 А2 и А1 А3 . 3) Площадь грани А1А2А3равна половине площади параллелограмма, построенного на векторах
Здесь определитель вычисляется с помощью разложения по первой строке. Следовательно,
4) Объем V пирамиды равен 1/6 объема параллелепипеда, построенного на векторах
.
Пример. Найти центры и привести к каноническому виду и построить кривые: 1) 2 x2 + 3 y2 - 4x + 6y - 7 = 0; 2) 2 x y = a2 Решение 1). B = 0, Выполним приведение к полному квадрату: 2 (x - 1)2 + 3 (y + 1)2 - 12 = 0 Координаты центра симметрии (1; - 1), линейное преобразование X = x - 1, Y = y + 1 приводит уравнение к каноническому виду X2 /6 + Y2 /4 = 1, где a = 2.48,b = 2 2). B = 1, Центр системы координат находится в центре симметрии кривой, т.к. в уравнении нет линейных членов. Совершим поворот осей на угол
|
= 1∙(-1)∙3 + (-5)∙(-1)∙(-2) + 2∙3∙2 - 2∙(-1)∙(-2) – (-5)∙3∙3 - 1∙(-1)∙2=42.
= - 42, ∆2 = 
= -42,, ∆3 = 
= 42.
. Преобразуем расширенную матрицу системы следующим образом.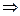
; В =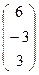 
.
. Транспонируем матрицу из алгебраических дополнений ||Ai j ||T = 
. Разделив каждый элемент транспонированной матрицы на определитель, получим обратную матрицу А-1 = 1/42 
= 
.
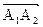=(1 - 3)i+ (-3 – (-2))j +(1 – 2)k= - 2i - 1j - k.
=(2 – 3) i +(0 –(- 2))j +(4 -2) k = - i + 2j + 2 k.
.
.
.
. Вектор 
= -72 
0,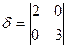 
= 6 > 0 - эллипс
= a2 
= - 1 < 0 - гипербола
.. По формуле (45) имеем tg 2 
= B/(A - C) = 
, т.е. 
1 
Уравнение 2х у = а2 описывает гиперболу с центром в (0;0). Оси симметрии располагаются по биссектрисам координатных углов, асимптотами служат оси координат, полуоси гиперболы равны а.
