Тереоретическое обоснование. 4
Текст программы.. 5 Вывод программы.. 6 Цель работы
1. Программная реализация на языке С++ интерполяционных формул Ньютона, с помощью которого найти приближенное значение заданной функции. 2. Проверка работы составленной программы для заданной функции.
Таблица функции (1 вариант)
Найти приближенное значение функции, при следующих значениях аргументов:
Теоретическое обоснование Пусть для функции
Условия (1) эквивалентны тому, что
Интерполяционный полином Ньютона имеет вид:
Легко видеть, что полином (2) полностью удовлетворяет требованиям поставленной задачи. Действительно, во-первых, степень полинома
Заметим, что при
Для практического использования интерполяционную формулу Ньютона (2) обычно записывают в несколько преобразованном виде. Для этого введём новую переменную
где
|
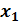
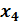
заданы значения 
для равноотстоящих значений независимой переменной: 
, 
, где 
- шаг интерполяции. Требуется подобрать полином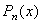 
степени не выше 
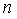, принимающий в точках 
значения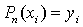
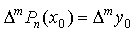при 
.
. (2)
и 
, 
.
формула (2) превращается в ряд Тейлора для функции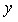 
:
.
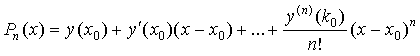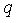по формуле 
; тогда получим:
, (3)
, исходя из точки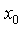 
. Это и есть окончательный вид интерполяционной формулы Ньютона.
