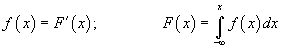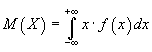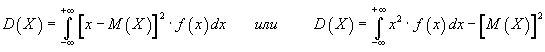Числовые характеристики дискретных случайных величин

Числовые характеристики дискретных случайных величин

Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности:
M(X) = x₁p₁ + x₂p₂ +... + x_np_n

Свойства математического ожидания.
1) Математическое ожидание постоянной величины равно самой величине:
М(С)= С
2) Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) = С·М(Х)
3) Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
М(Х₁ + Х₂ + …+ Х_n) = М(Х₁) + М(Х₂) +... + М(Х_n)
4) Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
М(Х₁ · Х₂ ·... · Х_n) = М(Х₁) · М(Х₂) ·... · М(Х_n)

13. Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания:
D(X) = (x₁ - M(X))²p₁ + (x₂ - M(X))²p₂ +... + (x_n- M(X))²p_n = x²₁p₁ + x²₂p₂ +... + x²_np_n - [M(X)]²

^14.

Свойства дисперсии.
1) Дисперсия постоянной величины равна нулю: D(С) = 0
2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С² · D(Х)
3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х₁ ± Х₂ ±... ± Х_n) = D(Х₁) + D(Х₂) +... + D(Х_n)

14. Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии:
σ(X) = √D(X)

15. Непрерывной называют случайную величину, которая может принимать любые значения из некоторого заданного интервала, например, время ожидания транспорта, температура воздуха в каком-либо месяце, отклонение фактического размера детали от номинального, и т.д. Интервал, на котором она задана, может быть бесконечным в одну или обе стороны.

16. Функция распределения случайной величины, она же интегральная функция распределения вероятностей - это функция, определяющая для каждого значения x вероятность того, что случайная величина (ξ) примет значение меньшее, чем x: F(x) = P(ξ < x). Численно функция распределения равна площади фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков - рассматриваемым интервалом.
Основные свойства:
1) Значения функции распределения лежат в интервале [0; 1], т.е. 0 ≤ F(X) ≤ 1
2) Это функция неубывающая, при x→-∞ F(X)→0, при x→+∞ F(X)→1
3) Вероятность попадания в интервал (a, b) определяется формулой F(b) - F(a)

Взаимосвязь интегральной и дифференциальной функций распределения вероятностей:

17) Математическое ожидание непрерывной случайной величины вычисляется по формуле:

В частности, если с.в. задана своей плотностью вероятности на каком-либо отрезке, то и интеграл вычисляем на этом отрезке.

Дисперсия непрерывной случайной величины вычисляется по формуле:

Относительно пределов интегрирования - то же самое.

Среднее квадратическое отклонение непрерывной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии:
σ(X) = √D(X)