Нормальное распределение. Нормальное распределение - распределение вероятностей, которое задается функцией плотности распределения:Нормальное распределение - распределение вероятностей, которое задается функцией плотности распределения:
где a - математическое ожидание, σ - среднее квадратическое отклонение. График плотности распределения для нормально распределённой случайной величины имеет вид, отдалённо напоминающий колокол:
Правило трёх сигм ( Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа: Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю. Это правило называется правилом трех сигм. Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
|
,
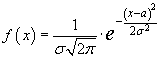) — практически все значения нормально распределённой случайной величины лежат в интервале 
. Более строго — не менее чем с 99,7 % достоверностью значениенормально распределенной случайной величины лежит в указанном интервале (при условии, что величина 
истинная, а не полученная в результате обработки выборки).Если же истинная величина 
, а s. Таким образом, правило трёх сигм преобразуется в правило трёх s.
