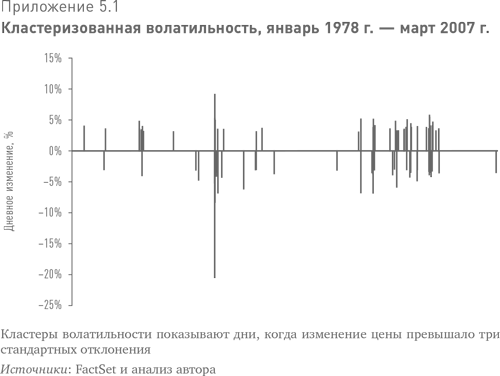
От неопределенности к вероятности

 

В своей книге «Просчитанный риск» (Calculated Risks) Гигеренцер предлагает три метода оценки вероятностей. Эти методы описаны в последовательности от менее конкретного к более конкретному и могут помочь инвесторам в классификации вероятностных суждений³:

 

1. Степени убеждения отражают субъективные вероятности и представляют собой наиболее «вольный» способ перевода неопределенности в вероятность. Суть этого способа в том, что инвесторы могут переводить даже единичные события в вероятности при соблюдении закона вероятности – все множество альтернатив сводится к одной. Кроме того, инвесторы могут часто обновлять свою оценку вероятностей на основе степеней убеждения при получении новой, относящейся к делу информации.

2. Предрасположенность. Вероятности на основе предрасположенности отражают свойства объекта или системы. Например, если игральная кость симметрична и сбалансированна, выпадение каждого числа имеет вероятность один к шести. Оценка риска в DASA и NASA, судя по всему, также основана на предрасположенности (свойствах). Данный метод оценки вероятности не всегда учитывает все факторы, которые могут повлиять на исход (такие как человеческие ошибки при запуске ракет).

3. Частота. В данном случае вероятности оцениваются на основе большого количества наблюдений в соответствующей референтной группе. При отсутствии надлежащей референтной группы оценка вероятности на основе частоты невозможна. Использующих этот метод игроков не интересуют ни чьи‑либо предположения о том, какое число может выпасть следующим, ни свойства кости. Они сосредоточивают свое внимание только на результатах повторных бросков кости.

 

Какое отношение это имеет к долгосрочной доходности фондового рынка? А такое, что много чернил потрачено на прогнозирование рынка на основе степеней убеждения, когда вероятностная оценка, однако, значительно искажается недавним опытом. Ведь степени убеждения насыщены эмоциями.

К фондовому рынку также можно подходить с позиций предрасположенности. Как пишет Джереми Сигел в своей книге «Долгосрочные инвестиции в акции» (Stocks for the Long Run), в США годовая доходность акций на протяжении 200 лет составляла чуть меньше 7 % с учетом всех неблагоприятных периодов⁴. Вопрос в том, существуют ли свойства, которые способствуют росту экономики и прибыли и поддерживают столь устойчивую доходность?

Наконец, фондовый рынок можно оценивать на основе частоты. Например, возьмем годовую доходность рынка за период с 1926 по 2006 г. Это распределение доходности имеет среднее арифметическое 12,0 % со стандартным отклонением 20,1 % (если применяется статистика нормального распределения). Предположив, что в будущем распределение годовой доходности останется таким же, как в прошлом (т. е. если считать последние 80 лет правомочной референтной группой), мы можем составить суждения о вероятностях будущей годовой доходности⁵.

Из трех вышеописанных методов оценки вероятностей академическое финансовое сообщество склоняется к последнему. Большинство финансовых моделей предполагает, что изменения цены подчиняются нормальному распределению. Например, в модели ценообразования опционов Блэка – Шоулза одним из ключевых входных параметров является волатильность или стандартное отклонение будущих изменений цены.

Но изменения цены акций не подчиняются нормальному распределению, что влияет на наши представления о риске и неопределенности, маркет‑тайминге и управлении активами. А конкретнее: изменения цены акций распределяются с высоким эксцессом – среднее значение выше, а хвосты толще, чем при нормальном распределении. (Мы все же должны признать, что существует распределение, характеризующее рынок; просто это ненормальное распределение.) Выбросы (экстремальные значения) доходности представляют собой особый интерес для понимания характеристик доходности фондового рынка по прошествии времени.

Чтобы проиллюстрировать эту мысль, я взял дневные изменения цены индекса S&P 500 за период с 3 января 1978 г. по 30 марта 2007 г. Годовая доходность индекса (без учета дивидендов) за этот период составила 9,5 %. Затем я исключил 50 худших и 50 лучших дней из выборки, составившей более 7000 дней. Если бы вам каким‑то образом удалось избежать 50 худших дней, то ваша годовая доходность выросла бы до 18,2 %, что почти на 9 % выше фактической. Но без 50 лучших дней ваша доходность составила бы всего 0,6 %.

Хотя этот анализ привлекает внимание, ему недостает контрольной точки. Чтобы обеспечить лучший контекст, я рассчитал среднее значение и стандартное отклонение на основе фактических базовых данных и использовал эту статистику для создания случайной выборки с таким же размером и характеристиками. Когда я исключил 50 худших дней из созданной мной выборки, доходность составила всего 15,2 % (по сравнению с 18,2 % для реальных данных). Аналогичным образом, когда я исключил 50 лучших дней, доходность составила 3,5 %, что существенно выше, чем для реальных данных.

Проще говоря, этот анализ показывает, что дни с экстремальными значениями доходности оказывают гораздо большее влияние на общую доходность рынка, чем предполагается нормальным распределением. Кроме того, это весомый аргумент против маркет‑тайминга – разве что у инвестора есть какой‑либо способ систематически предвидеть дни с экстремальной доходностью.

 

 

И последнее замечание по поводу дней с выбросами доходности: они не распределены в случайном порядке по временно́му ряду, а стремятся в кластеры (см. приложение 5.1). Наш анализ, исключивший дни с максимальной и минимальной доходностью, на самом деле не очень реалистичен, потому что в реальной жизни дни с экстремальной волатильностью идут группами.