 Приборы, служащие для измерения вязкости, называются вискозиметрами. В данной работе применяется вискозиметр, основанный на использовании метода Стокса, в основе которого лежат процессы, определяющие характер свободного движения твёрдого шарика, опущенного в жидкость. В этом случае на шарик действуют три силы (рис. 2).
Приборы, служащие для измерения вязкости, называются вискозиметрами. В данной работе применяется вискозиметр, основанный на использовании метода Стокса, в основе которого лежат процессы, определяющие характер свободного движения твёрдого шарика, опущенного в жидкость. В этом случае на шарик действуют три силы (рис. 2).
Рис. 2
1) сила тяжести Р, направленная вертикально вниз и равная
 (1)
(1)
(где r – радиус шарика,  - плотность материала шарика при данной температуре; g – ускорение свободного падения).
- плотность материала шарика при данной температуре; g – ускорение свободного падения).
2) сила Архимеда FA, направленная вертикально вверх и равная весу жидкости, вытесненной шариком,
 (2)
(2)
(где  - плотность жидкости при данной температуре).
- плотность жидкости при данной температуре).
3) сила внутреннего трения Fтр направлена в сторону, обратную скорости движения (в нашем случае вертикально вверх); ее можно рассчитать по формуле Стокса:
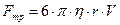 (3)
(3)
(где V – скорость равномерного движения шарика;  - коэффициент внутреннего трения).
- коэффициент внутреннего трения).
Силы P и FA постоянны, а Fтр растет с увеличением скорости шарика. Это происходит до тех пор, пока равнодействующая всех сил не станет равной нулю:
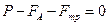 . (4)
. (4)
Начиная с этого момента шарик движется равномерно.
Подставляя (1), (2) и (3) в уравнение (4), получим условие равномерного движения шарика в виде:

Заменив в полученном соотношении радиус шарика на его диаметр  , а скорость установившегося движения шарика по отношению пройденного пути l к затраченному на его прохождение времени
, а скорость установившегося движения шарика по отношению пройденного пути l к затраченному на его прохождение времени 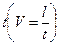 , получаем окончательное выражение для расчета коэффициента вязкости жидкости:
, получаем окончательное выражение для расчета коэффициента вязкости жидкости:
 (5)
(5)
Уравнение (5) справедливо для случая, когда шарик падает в безграничной среде. Если шарик движется вдоль оси трубки, то необходимо учитывать влияние стенок трубки. Это влияние обусловлено тем, что молекулы слоя жидкости, прилегающие к внутренним стенкам трубки, «прилипают» к ней и не перемещаются.
 Вискозиметр, используемый в данной работе (рис.3), представляет собою стеклянный цилиндрический сосуд, закрепленный в держателе и расположенный строго вертикально. Нижний конец сосуда запаян, а на верхнем имеется воронка с отверстием строго по осевой линии цилиндра, предназначенная для зарядки вискозиметра исследуемой жидкостью и для придания направления движения твердых шариков, опускаемых в жидкость. На цилиндре имеются две метки (А и Б), способные перемещаться вдоль него. Внутренний диаметр вискозиметра значительно превосходит диаметр маленьких твердых шариков, поэтому влиянием вискозиметра на их движение можно пренебречь.
Вискозиметр, используемый в данной работе (рис.3), представляет собою стеклянный цилиндрический сосуд, закрепленный в держателе и расположенный строго вертикально. Нижний конец сосуда запаян, а на верхнем имеется воронка с отверстием строго по осевой линии цилиндра, предназначенная для зарядки вискозиметра исследуемой жидкостью и для придания направления движения твердых шариков, опускаемых в жидкость. На цилиндре имеются две метки (А и Б), способные перемещаться вдоль него. Внутренний диаметр вискозиметра значительно превосходит диаметр маленьких твердых шариков, поэтому влиянием вискозиметра на их движение можно пренебречь.
Наблюдая за характером равномерного движения шарика в жидкости и используя соотношение (5), можно определить коэффициент внутреннего трения жидкости.

 Приборы, служащие для измерения вязкости, называются вискозиметрами. В данной работе применяется вискозиметр, основанный на использовании метода Стокса, в основе которого лежат процессы, определяющие характер свободного движения твёрдого шарика, опущенного в жидкость. В этом случае на шарик действуют три силы (рис. 2).
Приборы, служащие для измерения вязкости, называются вискозиметрами. В данной работе применяется вискозиметр, основанный на использовании метода Стокса, в основе которого лежат процессы, определяющие характер свободного движения твёрдого шарика, опущенного в жидкость. В этом случае на шарик действуют три силы (рис. 2). (1)
(1) - плотность материала шарика при данной температуре; g – ускорение свободного падения).
- плотность материала шарика при данной температуре; g – ускорение свободного падения). (2)
(2) - плотность жидкости при данной температуре).
- плотность жидкости при данной температуре).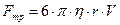 (3)
(3) - коэффициент внутреннего трения).
- коэффициент внутреннего трения).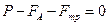 . (4)
. (4)
 , а скорость установившегося движения шарика по отношению пройденного пути l к затраченному на его прохождение времени
, а скорость установившегося движения шарика по отношению пройденного пути l к затраченному на его прохождение времени 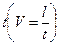 , получаем окончательное выражение для расчета коэффициента вязкости жидкости:
, получаем окончательное выражение для расчета коэффициента вязкости жидкости: (5)
(5) Вискозиметр, используемый в данной работе (рис.3), представляет собою стеклянный цилиндрический сосуд, закрепленный в держателе и расположенный строго вертикально. Нижний конец сосуда запаян, а на верхнем имеется воронка с отверстием строго по осевой линии цилиндра, предназначенная для зарядки вискозиметра исследуемой жидкостью и для придания направления движения твердых шариков, опускаемых в жидкость. На цилиндре имеются две метки (А и Б), способные перемещаться вдоль него. Внутренний диаметр вискозиметра значительно превосходит диаметр маленьких твердых шариков, поэтому влиянием вискозиметра на их движение можно пренебречь.
Вискозиметр, используемый в данной работе (рис.3), представляет собою стеклянный цилиндрический сосуд, закрепленный в держателе и расположенный строго вертикально. Нижний конец сосуда запаян, а на верхнем имеется воронка с отверстием строго по осевой линии цилиндра, предназначенная для зарядки вискозиметра исследуемой жидкостью и для придания направления движения твердых шариков, опускаемых в жидкость. На цилиндре имеются две метки (А и Б), способные перемещаться вдоль него. Внутренний диаметр вискозиметра значительно превосходит диаметр маленьких твердых шариков, поэтому влиянием вискозиметра на их движение можно пренебречь.


