Общая теория относительностиОсновная статья: Общая теория относительности Общая теория относительности — теория гравитации, разработанная Эйнштейном в 1905—1917 годах. Является дальнейшим развитием специальной теории относительности. В общей теории относительности постулируется, что гравитационные эффекты обусловлены не силовым взаимодействием тел и полей, а деформацией самого пространства-времени, в котором они находятся. Эта деформация связана, в частности, с присутствием массы-энергии.
Общая теория относительности отличается от других метрических теорий тяготения использованием уравнений Эйнштейна для связи кривизны пространства-времени с присутствующей в нём материей.
ОТО в настоящее время — самая успешная теория гравитации, хорошо подтверждённая наблюдениями.
Матричная квантовая механика Материал из Википедии — свободной энциклопедии Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 июля 2014; проверки требует 1 правка.
Матричная механика — математический формализм квантовой механики, разработанный Вернером Гейзенбергом, Максом Борном и Паскуалем Иорданом в 1925 году. Матричная механика была первой независимой и последовательной квантовой теорией. Она развивает идеи теории Бора, в частности отвечает на вопрос, как происходят квантовые переходы. Основная идея матричной механики заключается в том, что физические величины, характеризующие частицу, описываются матрицами, изменяющимися во времени. Такой подход вполне эквивалентный волновой механике Эрвина Шредингера и является основой для бра-кет нотации Дирака для волновой функции. Математический аппарат В матричной механике считается, что физическая система может находиться в одном из дискретного набора состояний n или в суперпозиции этих состояний, поэтому в целом состояние квантовомеханической системы задается вектором состояния: конечной или бесконечной совокупностью комплексных чисел
а каждой физической величине A, которую можно наблюдать в эксперименте, соответствует определенная матрица
Реальным физическим величинам соответствуют самосопряженные матрицы, для которых
Комплексные величины Особое место занимает матрица энергии H. Уравнение движения Матрица, которая описывает физическую величину, удовлетворяет уравнению движения
где частная производная задает явную зависимость физической величины от времени, а квадратные скобки означают коммутатор матриц A и H. В этой формуле i — мнимая единица Эквивалентность матричной механики и волновой механики Как показал Джон фон Нейман, матричная механика полностью эквивалентна волновой механике Шредингера. Эквивалентность вытекает из того, что волновую функцию
Коэффициенты этого разложения Матрица, которая соответствует определенной физической величине A задается матричными элементами оператора
Учитывая эквивалентность формулировок, в современной квантовой механике матричный подход используется на равных с описанием с помощью волновых функций.
|
Квантовая механика
,
.
задают амплитуду вероятности того, что квантовомеханическая система находится в состоянии n. Диагональные элементы матрицы A соответствуют значениям физической величины, когда она находится в определенном состоянии, а недиагональные элементы описывают вероятность переходов системы из одного состояния в другое.
,
—приведенная постоянная Планка. Если матрица A известна в начальный момент времени, то, решая данное уравнение, можно определить ее в любой момент времени.
можно разложить в ряд, используя определенный ортонормированной базис функций 
:
.
.
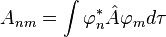