Описание алгоритма
Немецкий математик А. Гурвиц нашел косвенные условия оценки устойчивости линейных систем, которые позволяют составить алгоритм оценки устойчивости, не прибегая к нахождению корней. Алгоритм Гурвица основан на построении из коэффициентов характеристического уравнения (1) специальной матрицы — матрицы Гурвица. В соответствии с критерием Гурвица корни характеристического уравнения будут иметь отрицательные вещественные части, т. е. сама система будет устойчивой, если определитель матрицы Гурвица и определители всех ее диагональных, миноров положительны. Матрица Гурвица имеет следующий вид:
... … Правила для составлени матрицы Гурвица таковы: в первой строке выписываются коэффициенты характеристического уравнения с нечетными индексами, во второй — с четными. Последующие пары строк матрицы получают из первых двух, смещая их элементы на 1, 2, 3,... столбца. Образующиеся свободные места слева, а также те элементы, которые находятся в строке справа от an-1, an, заполняются нулями. Таким образом, матрица Гурвица имеет п строк и п столбцов. По главной диагонали располагаются коэффициенты характеристического уравнения начиная с а 1и до ап. Диагональные миноры
Таким образом, сами вычисления по алгоритму Гурвица состоят из следующих основных этапов: 1. Составление определителя Гурвица 2. Вычисление определителей 3. Анализ условия положительности определителей С помощью алгоритма Гурвица нетрудно показать, что критерием устойчивости системы с характеристическим уравнением первого или второго порядка является положительность коэффициентов этого уравнения. Рассмотрим работу алгоритма Гурвица на следующем примере. Исследовать устойчивость системы с характеристическим уравнением
а также все миноры
Произведем необходимые вычисления
Так как определитель Гурвица и его диагональные миноры больше нуля, то можно сделать вывод об устойчивости рассматриваемой системы. Как уже указывалось выше, критерий Гурвица дает необходимые и достаточные условия устойчивости линейных систем. На практике часто оказывается полезным использовать необходимое условие устойчивости — положительность всех коэффициентов характеристического уравнения при a0>0: ai>0,..., аn>0 (при a0<0 необходимое условие — отрицательность всех коэффициентов). Сформулированное условие позволяет сравнительно просто, минуя громоздкие вычисления, сделать вывод о неустойчивости системы.
|

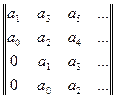 .
. (k=n— 1,..., 1) получаются из определителя матрицы Гурвица
(k=n— 1,..., 1) получаются из определителя матрицы Гурвица  путем вычеркивания справа и снизу Последовательно по одной строке и одному столбцу, по две строки и два столбца и т. д. Условие устойчивости.системы заключается в том, чтобы при а0>0 все диагональные миноры были положительны:
путем вычеркивания справа и снизу Последовательно по одной строке и одному столбцу, по две строки и два столбца и т. д. Условие устойчивости.системы заключается в том, чтобы при а0>0 все диагональные миноры были положительны: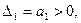
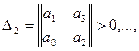
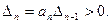 (2)
(2)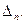
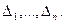
 В соответствии с описанным алгоритмом составим определитель Гурвица
В соответствии с описанным алгоритмом составим определитель Гурвица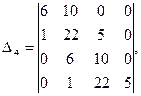


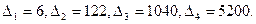 .
.


