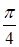Производная функции.
Упражнение 1. Найти производные функций: 1. y = x4 2. f(x) = 3x5 3. y = 4x-2 4. s = 5. f(x) = 6. y = 3x3(x2 - 7x + 4) 7. y = 2 10. y= 12. f(x) = 3x3 13. y = 16. y = 18. f(t) = 20. f(x) = 22. y = Упражнение 2. Уравнения касательной и нормали к кривой.
1. Составить уравнения касательной и нормали к графику функции f(x) = x2 + 4x + 5 в точке с абсциссой x = -3. 2. К графику функции f (x) = x + 3x2 в её точке с абсциссой x = -1 проведены касательная и нормаль. Составьте их уравнения. Упражнение 3. Физические приложения производной. 1. Движение точки, движущейся прямолинейно, задано уравнением s = t3 + 5t2 + 4. Найдите скорость и ускорение в момент t = 2с 2. Найдите ускорение точки, если скорость точки, движущейся прямолинейно, задана уравнением v = t2 + t – 1 в момент t = 3c 3. Точка движется прямолинейно по закону s = 6t – t2. В какой момент времени скорость точки окажется равной нулю? 4. Точка движется прямолинейно по закону s = t2 – 8t + 4. В какой момент времени скорость точки окажется равной нулю? 5. Закон изменения температуры Т тела в зависимости от времени t задан уравнением Т = 0,2t2. С какой скоростью нагревается это тело в момент времени t = 10? 6. Температура тела T изменяется в зависимости от времени t по закону Т = 0,5t2 - 2t. С какой скоростью нагревается это тело в момент времени t = 5? 7. Тело массой 10 кг. движется прямолинейно по закону s = 3t3 + t + 4. Найти кинетическую энергию тела (mv2/2) через 4с после начала движения. 8. Тело массой 100кг. движется прямолинейно по закону s=5t2 – 2. Найдите кинетическую энергию тела через 2с после начала движения. 9. Сила тока I изменяется в зависимости от времени t по закону I=0,4t2 (I - в амперах, t - в секундах). Найдите скорость изменения силы тока в конце 8-ой секунды. 10. Изменение силы тока I в зависимости от времени t дано уравнением I=2t2-5t (I - в амперах, t - в секундах). Найдите скорость изменения силы тока в конце 10-ой секунды. 11. Точка движется прямолинейно по закону S= 12. Движение точки задано уравнением S = t2 - 4t + 20. В какой момент времени скорость точки будет равна нулю?
Упражнение 4. Производная сложной функции. Найти производные функции: 1. y = (2x3-4x2+x)7 2. y = (x3-1)7 3. y = 1/(x2-1)4
4. f(x) =
6. y =
9. y = x2·
Упражнение 5.Производная логарифмической функции. Найти производные функций: 1. y = ln(x3-4x+5) 2. y = lg(3x2-x3) 3. y=ln((2x-x3)4·(1-x5)) 4. y = ln 5. f(x)=2lg(x+1) Найти f'(1) 6. y = ln Упражнение 6. Производная показательной функции. Найти производные функций: 1. y = 2-x 2. y = x·e2x 3. y = e-x Упражнение 7.Производные тригонометрических функций. Найти производные функций: 1. y = sin7x 2. y = tg4x 3. y = cos5x 4. y = tgx-ctg2x 5. y = sin3x 6. y = -1/4 cos4x 7. f(x)= -ctg5x Найти f' 8. y = 11. y = cosx-1/3 cos3x 12.Точка движется прямолинейно по закону S = a·cos а) Скорость движения точки при t = б) При каких значениях t скорость точки равна 0
13. Точка движется прямолинейно по закону S = sin2t. Найти время t, когда ускорение равно 0. Найти скорость движения в этот момент времени.
|


 Найти f'(3)
Найти f'(3)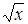 8. y =
8. y =  9. y = x2
9. y = x2  11. f(x) =
11. f(x) =  Найти f'(1)
Найти f'(1)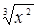
 14. y =
14. y =  15. y =
15. y = 
 17. y = x(
17. y = x( Найти y'(4,2)
Найти y'(4,2) Найти f'(8) 19. y =
Найти f'(8) 19. y = 
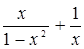 21. y =
21. y = 
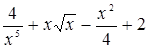 23. f(x) =
23. f(x) = 
 . Найти её скорость в момент t =2,25.
. Найти её скорость в момент t =2,25. 5. f(t) = `t2 - t + 1 Найдите f'(2)
5. f(t) = `t2 - t + 1 Найдите f'(2)
 7. y =
7. y =  8. f(x)=
8. f(x)= 
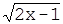 10. f(x) = (t2+1)·
10. f(x) = (t2+1)· 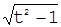 11. f(x) =
11. f(x) = 
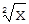

 4 f(x) =
4 f(x) =  Найти f'(-1)
Найти f'(-1)
 9. y = sin4x·cosx 10. y = tg53x-sin4x
9. y = sin4x·cosx 10. y = tg53x-sin4x . Найти:
. Найти: