Квантовая механика
3.1. Какие явления объясняются квантовым характером излучения и поглощения 1) явление интерференции 2) явление дифракции 3) наличие линейчатых спектров 4) явление фотоэффекта 3.2. Что является источником линейчатых спектров испускания? 1) атомарные газы 2) жидкости 3) твердые тела 4) молекулярные газы 3.3. Что является источником полосатых спектров испускания? 1) атомарные газы 2) жидкости 3) твердые тела 4) молекулярные газы 3.4. Выберите верные утверждения. 1) состояние электрона в атоме характеризуется тремя квантовыми числами 2) принцип Паули справедлив только для фермионов 3) магнитное спиновое квантовое число может иметь только два значения 3.5. Выберите верные утверждения. 1) инверсная населенность – это такое заполнение электронами энергетических уровней, при котором нарушается принцип Паули 2) инверсная населенность – это состояние, при котором возбужденных атомов в веществе больше, чем невозбужденных 3) когерентность лазерного излучения обусловлена индуцированными переходами 4) когерентность лазерного излучения обусловлена спонтанными переходами
3.16. Кому принадлежит идея о том, что все микрочастицы обладают волновыми свойствами? 1) Планку 2) Бору 3) Резерфорду 4) де Бройлю 3.17. Укажите верное утверждение. 1) групповая скорость волны де Бройля не имеет смысла как физическая величина 2) групповая скорость волны де Бройля равна скорости частицы 3) групповая скорость волны де Бройля зависит от квадрата длины волны 4) групповая скорость волны де Бройля больше скорости света в вакууме 5) групповая скорость волны де Бройля равна скорости света в вакууме 3.18. Укажите частицу, обладающую наименьшей длиной волны, если скорости частиц одинаковы. 1) альфа-частицы 2) электроны 3) нейтроны 4) протоны 3.19. Два источника излучают свет с длиной волны 375 нм и 750 нм. Чему равно отношение импульсов фотонов, излучаемых первым и вторым источником? 3.20. Чему равно отношение длин волн де Бройля протона и нейтрона, если они двигаются с одинаковыми скоростями? 3.21. Найдите отношение скоростей протона и альфа-частицы, длины волн де Бройля которых одинаковы. 3.22. Отношение скоростей двух микрочастиц 3.23. Позитрон, протон, нейтрон и альфа-частица имеют одинаковую длину волны де Бройля. Какая частица обладает наибольшей скоростью? 3.24. Протон и дейтрон прошли одинаковую ускоряющую разность потенциалов. Чему равно отношение их длин волн де Бройля? 3.25. В опыте Дэвиссона и Джермера исследовалась дифракция прошедших ускоряющее напряжение электронов на монокристалле никеля. Как изменится длина волны де Бройля электрона, если ускоряющее напряжение уменьшить в 2 раза? 3.26. Чему равно отношение длин волн де Бройля для дейтрона и альфа-частицы, если они прошли одинаковую ускоряющую разность потенциалов? 3.27. Электрон локализован в пространстве в пределах Δ х =1,0 мкм. Учитывая, что постоянная Планка ħ;=1,05·10-34 Дж·с, а масса электрона m =9,1·10-31 кг, найдите наименьшее значение неопределенности скорости Δ υ;x (в м/с). 3.28. Положение пылинки массой m =10-9 кг можно установить с неопределенностью Δ х =0,1 мкм. Учитывая, что постоянная Планка ħ;=1,05·10-34 Дж·с, найдите наименьшее значение неопределенности скорости Δ υ;x (в м/с). 3.29. Найдите отношение неопределенностей проекций скоростей нейтрона и альфа-частицы на некоторое направление при условии, что соответствующие координаты частиц определены с одинаковой точностью. 3.30. Положение бусинки массой 1 г и электрона (m ≈10-30 кг) определены с одинаковой погрешностью 10-7 м. Квантовомеханическая неопределенность х-компоненты скорости бусинки составляет примерно 10-24 м/с. Какова неопределенность х-компоненты скорости электрона? 3.31. Высокая монохроматичность лазерного излучения обусловлена относительно большим временем жизни электронов в метастабильном состоянии ~10-3 с. Учитывая, что постоянная Планка ħ;=6,6·10-16 эВ·с, найдите ширину метастабильного уровня (в эВ). 3.32. Высокая монохроматичность лазерного излучения обусловлена относительно большим временем жизни электронов в метастабильном состоянии ~10-3 с. Учитывая, что постоянная Планка ħ;=1,05·10-34 Дж·с, найдите ширину метастабильного уровня (в эВ). 3.33. Среднее время жизни 3.34. Что можно определить с помощью волновой функции, являющейся решением уравнения Шредингера? 1) вероятность того, что частица находится в определенной области пространства 2) траекторию частицы 3) местонахождение частицы 4) средние значения физических величин, характеризующих частицу 3.35. Задана пси-функция 1) 3) 5) 3.36. Укажите стационарное уравнение Шредингера для электрона в водородоподобном ионе. 1) 3) 3.37. Укажите стационарное уравнение Шредингера для частицы в потенциальном поле. 1) 3) 3.38. Укажите стационарное уравнение Шредингера для линейного гармонического осциллятора. 1) 3) 3.39. Какое уравнение описывает движение частицы в трехмерном бесконечно глубоком потенциальном ящике? 1) 3) 3.40. Какое уравнение описывает движение частицы вдоль оси ОХ под действием квазиупругой силы? 1) 3) 3.41. Укажите нестационарное уравнение Шредингера. 1) 3) 3.42. Какое уравнение описывает одномерное движение свободной частицы? 1) 3) 3.43. Установите соответствие между квантовомеханическими задачами и уравнениями Шредингера для них.
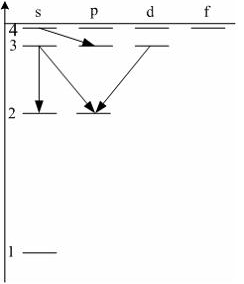
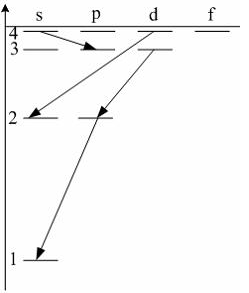
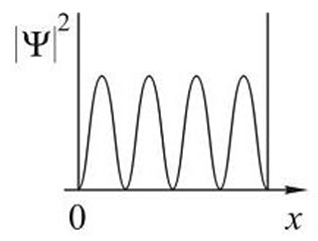
3.44. Стационарное уравнение Шредингера имеет вид: 1) электрон в водородоподобном атоме 2) движение свободной частицы 3) электрон в трехмерном потенциальном ящике 4) линейный гармонический осциллятор 3.45. Стационарное уравнение Шредингера имеет вид: 1) частицу в трехмерном потенциальном ящике с бесконечно высокими стенками 2) частицу в одномерном потенциальном ящике с бесконечно высокими стенками 3) электрон в атоме водорода 4) линейный гармонический осциллятор 3.46. Какие утверждения верны для уравнения Шредингера: 1) уравнение стационарно 2) уравнение соответствует трехмерному случаю 3) уравнение характеризует состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике 4) уравнение характеризует движение частицы вдоль оси ОХ под действием квазиупругой силы, пропорциональной смещению частицы от положения равновесия 3.47. На рисунках приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Какой рисунок соответствует состоянию с квантовым числом п= 1, п= 2, п= 3, п= 4?
3.55. На рисунках схематически представлены графики распределения плотности вероятности обнаружения электрона по ширине одномерного потенциального ящика с бесконечно высокими стенками для состояний с различными значениями главного квантового числа n. Чему равна вероятность обнаружить электрон в интервале от
3.56. На рисунках схематически представлены графики распределения плотности вероятности обнаружения электрона по ширине одномерного потенциального ящика с бесконечно высокими стенками для состояний с различными значениями главного квантового числа n. Чему равно отношение вероятности обнаружить электрон на первом энергетическом уровне в левой половине ящика к вероятности обнаружить электрон на четвертом энергетическом уровне в интервале от
2) если энергия частицы меньше высоты барьера (Е < U0), то частица отразится от барьера и будет двигаться в обратном направлении; проникнуть сквозь барьер она не может 3) если энергия частицы больше высоты барьера (Е > U0), частица беспрепятственно пройдет над барьером 4) если энергия частицы меньше высоты барьера (Е < U0), то есть отличная от нуля вероятность того, что частица проникнет сквозь барьер и окажется в области, где х > l 3.58. Собственные функции электрона в атоме водорода 1) модуль орбитального момента импульса электрона 2) проекцию орбитального момента импульса электрона на некоторое направление 3) модуль собственного момента импульса электрона 4) энергию электрона в атоме водорода 3.59. Собственные функции электрона в атоме водорода 1) модуль орбитального момента импульса электрона 2) проекцию орбитального момента импульса электрона на некоторое направление 3) модуль собственного момента импульса электрона 4) энергию электрона в атоме водорода
|




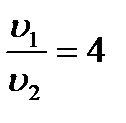 . Чему равно отношение масс этих частиц
. Чему равно отношение масс этих частиц 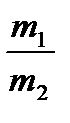 , если их длины волн де Бройля удовлетворяют соотношению
, если их длины волн де Бройля удовлетворяют соотношению 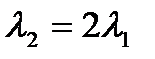 ?
?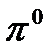 -мезона равно 1,9·10-16 с. Какова наименьшая энергетическая разрешающая способность прибора, с помощью которого можно зарегистрировать
-мезона равно 1,9·10-16 с. Какова наименьшая энергетическая разрешающая способность прибора, с помощью которого можно зарегистрировать  частицы. Каким выражением определяется вероятность того, что частица будет обнаружена в объёме V?
частицы. Каким выражением определяется вероятность того, что частица будет обнаружена в объёме V? 2)
2) 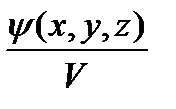
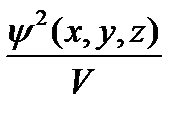 4)
4) 
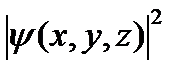
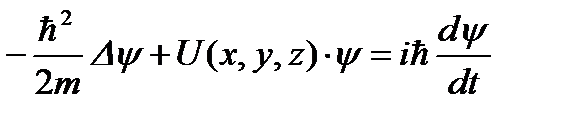 2)
2) 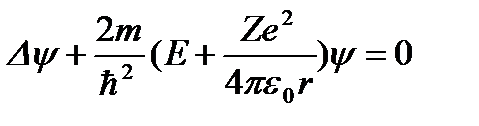
 4)
4) 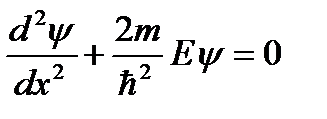
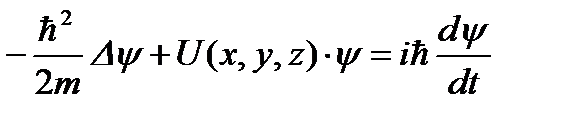 2)
2) 
 4)
4) 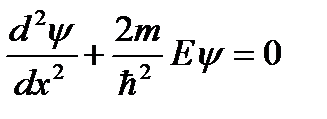
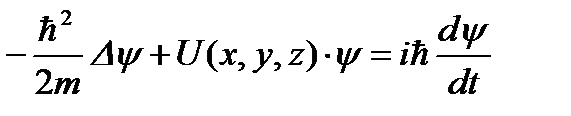 2)
2) 
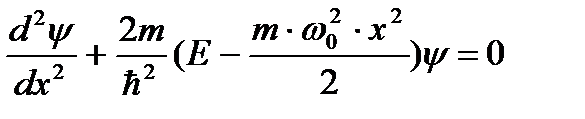 4)
4) 
 2)
2) 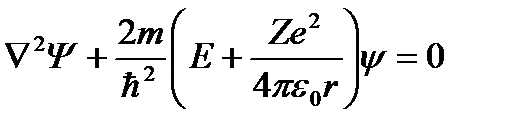
 4)
4) 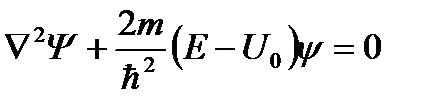
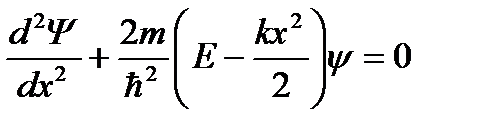 2)
2) 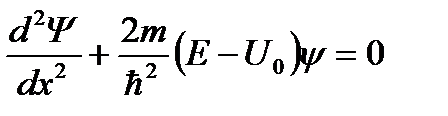
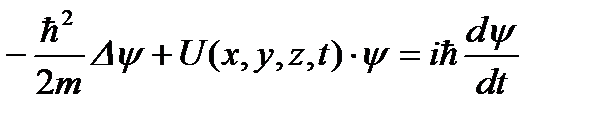 2)
2) 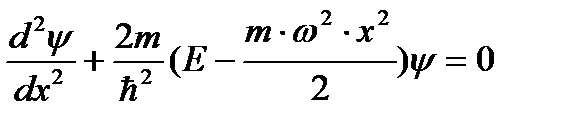 ?
?
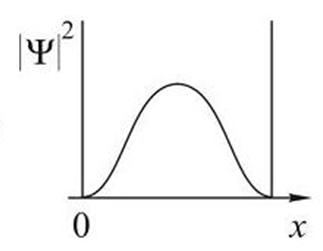
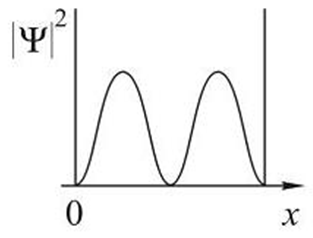
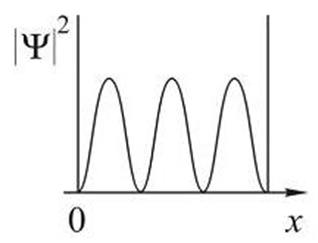
 < х <
< х < 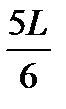 ?
?
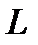 ?
?
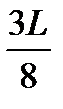 < х <
< х < 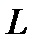 ?
?
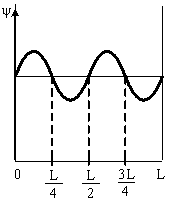
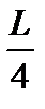 < х <
< х <  ?
?
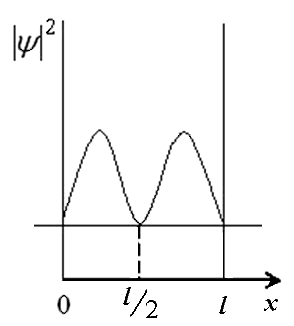
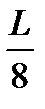 < х <
< х < 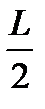 ?
?
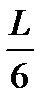 < х <
< х < 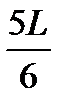 ?
?
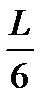 < х <
< х < 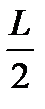 ?
?
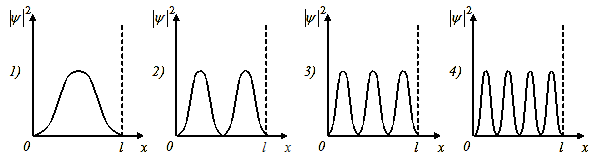
 до
до 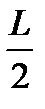 ?
?
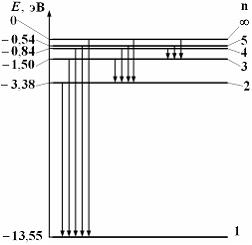
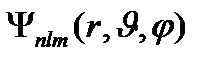 содержат три целочисленных параметра n, l и m. Параметр n называется главным квантовым числом, параметры l и m – орбитальным и магнитным квантовыми числами соответственно. Что определяет магнитное квантовое число m?
содержат три целочисленных параметра n, l и m. Параметр n называется главным квантовым числом, параметры l и m – орбитальным и магнитным квантовыми числами соответственно. Что определяет магнитное квантовое число m?


