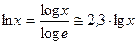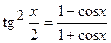Авторы- составители:
Кирко Г.Е., Кустова Я.Р., Афанасьев А.Л., Корякина А.Г., Смирнова З.А., Зернина Н.В., Сазонова Н.К., Черемных М.Р.
Редактор Н.А. Щепина
Корректор Е.М. Сторожева
Подписано в печать 2009.
Формат 60х90/16.Усл. печ. л.____________
Тираж ______________экз. Заказ № ___________
Редакционно- издательский отдел
ГОУ ВПО ПГМА им. ак. Е.А. Вагнера Росздрава
614990, г. Пермь,ул. Большевистская,85
Отпечатано в
[1] Использовать формулы двойного аргумента
[2] Использовать формулу 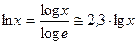
[3] Использовать формулу половинного аргумента: 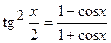
[4] Решения приведенных заданий в главах 4,5,6 даны в конце настоящего пособия.
[5] Таблицы измерений роста выдаются преподавателем.
СОДЕРЖАНИЕ
|
| Стр
|
| Глава I.
| Пределы
|
|
| Глава 2.
| Дифференциальное исчисление функций одной независимой переменной
|
|
|
| §1.
| Понятие производной
|
|
|
| §2.
| Основные правила дифференцирования. Дифференцирование основных элементарных функций.
|
|
|
| §3.
| Дифференцирование сложной функции
|
|
|
| §4.
| Производные высших порядков
|
|
|
| §5.
| Дифференциал функции
|
|
|
| §6.
| Применение производной при решении прикладных задач
|
|
| Глава 3.
| Исследование функций методами дифференциального исчисления
|
|
| §1.
| Интервалы монотонности функции
|
|
|
| §2.
| Экстремум функции
|
|
| Глава 4.
| Неопределенный интеграл
|
|
|
| §1.
| Непосредственное интегрирование
|
|
|
| §2.
| Интегрирование способом подстановки
(методом замены переменной)
|
|
|
| §3.
| Интегрирование по частям
|
|
|
| §4.
| Применение неопределенного интеграла при решении прикладных задач
|
|
| Глава 5.
| Определенный интеграл
|
|
|
| §1.
| Определенный интеграл и его непосредственное интегрирование
|
|
|
| §2.
| Приложение определенного интеграла для вычисления площадей плоских фигур
|
|
|
| §3.
| Приложение определенного интеграла к решению физических задач.
|
|
| Глава 6.
| Дифференциальные уравнения
|
|
|
| §1.
| Основные понятия
|
|
|
| §2.
| Уравнения с разделяющимися переменными
|
|
|
| §3.
| Однородные дифференциальные уравнения
|
|
|
| §4.
| Задачи на составление дифференциальных уравнений
|
|
| Глава 7.
| Элементы теории вероятностей и математической статистики
|
|
|
| §1.
| Основные понятия
|
|
|
| §2.
| Числовые характеристики распределения случайных величин
|
|
|
| §3.
| Нормальный закон распределения случайных величин
|
|
|
| §4.
| Генеральная совокупность. Оценка параметров генеральной совокупности по ее выборке
|
|
|
| §5.
| Интервальная оценка. Интервальная оценка при малой выборке. Распределение Стьюдента
|
|
|
| §6.
| Проверка гипотез. Критерии значимости.
|
|
|
| §7.
| Элементы корреляционного и регрессионного анализа.
|
|
|
|
| 7.1. Характер взаимосвязи между признаками
|
|
|
|
| 7.2. Проведение корреляционного анализа с помощью коэффициента парной корреляции
|
|
|
|
| 7.3. Элементы регрессионного анализа
|
|
| Лабораторные работы по статистической обработке результатов
|
|
|
| 1.
| Статистическая обработка данных измерения роста
|
|
|
| 2.
| Задания для проведения статистического анализа совокупности данных
|
|
| Приложение.
|
|
|
|
| П1.
| Правила приближенных вычислений
|
|
|
| П1.1
| Запись приближенных чисел
|
|
|
| П1.2.
| Правила округления
|
|
|
| П1.3.
| Вычисление с приближенными числами
|
|
| Ответы.
|
|
|
| Список литература
|
|
| | | | | |
«Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой»
Леонардо да Винчи,
G.36v (Записная книжка, 186 страница)
Глава 1