ВВЕДЕНИЕ. Рассмотрим механизм возникновения внутреннего трения (вязкости) в жидкостях
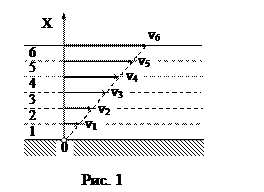
Рассмотрим механизм возникновения внутреннего трения (вязкости) в жидкостях. Молекулы в жидкостях, интенсивно взаимодействуя между собой, находятся на значительно меньших расстояниях относительно друг друга, чем молекулы газа. Характер теплового (хаотического) движения молекул в жидкостях существенно отличается от теплового движения молекул газа. Молекулы жидкости большую часть времени колеблются около своего положения равновесия. Вследствие хаотичности движения скорости и амплитуды колебаний соседних молекул различны, и время от времени соседние молекулы расходятся настолько, что некоторые из них оказываются на расстояниях порядка диаметра молекул (перескакивают) и начинают колебаться около нового положения равновесия. При течении реальной жидкости отдельные слои ее воздействуют друг на друга с силами, касательными к этим слоям. Это явление называют внутренним трением или Рассмотрим течение вязкой жидкости по горизонтальному руслу (рис. 1). Условно представим жидкость в виде нескольких слоев 1, 2, 3, 4, 5, 6. Слой вязкой жидкости, непосредственно граничащий с горизонтальным руслом, «прилипает» к нему и неподвижен. По мере удаления от дна скорость слоев жидкости нарастает (v1<v2<v3<v4<v5<v6). Максимальная скорость будет у слоя, который граничит с воздухом. Слои воздействуют друг на друга. Более быстрый слой ускоряет соседний с ним более медленный и, наоборот, более медленный задерживает более быстрый. Вязкость проявляется в форме силы, препятствующей относительному движению слоев жидкости, касательной к слоям. Сила внутреннего трения, действующая между двумя слоями, пропорциональна площади соприкосновения взаимодействующих слоев и тем больше, чем больше их относительная скорость. Принято выражать силу в зависимости от изменения скорости, приходящегося на единицу длины в направлении, перпендикулярном скорости, т.е. от величины dv/dy, называемой градиентом скорости (формула Ньютона): F = h Величина h (греческая буква «эта») называется коэффициентом внутреннего трения или коэффициентом динамической вязкости. Если в (1) положить численно dv/dy = 1 и S = 1, то h = F, т.е. коэффициент динамической вязкости численно равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоев, движущихся один относительно другого с градиентом скорости, равным единице. В системе СИ (кг, м, с и т.д.) h измеряется в Па×с. Это такая вязкость, при которой на слой площадью в 1 м 2 действует сила в 1 Н при градиенте скорости 1 м/с на каждый метр длины. В системе СГС (г, см, с, и т.д.) h измеряется в Пз (Пуазах). Из молекулярно-кинетической теории следует, что существование внутреннего трения связано с переносом количества движения молекулами из слоя в слой вследствие теплового движения. В газах перенос количества движения происходит при переходе молекул из одного слоя в другой, что и определяет внутреннее трение между слоями. В жидкостях молекулы большую часть времени находятся около положения равновесия и этот механизм играет незначительную роль. Основной причиной возникновения сил трения в жидкостях является сильное взаимодействие между молекулами отдельных слоев. Движущийся слой жидкости увлекает соседние слои в основном за счет сил сцепления. Коэффициент вязкости жидкости зависит от природы жидкости и от температуры. С ростом температуры коэффициент вязкости жидкости уменьшается (у газов возрастает). Зависимость его от температуры жидкости дается формулой Френкеля: h = B×exp( здесь B - константа, k - постоянная Больцмана, Е - энергия активации: минимальная энергия, необходимая молекуле для преодоления сил взаимодействия с ближайшим окружением и перескока в новое положение равновесия. Величина Е ~ (2-3)*10-20 Дж, поэтому при нагревании жидкости на 10 градусов вязкость падает на 20-30%. В таблице 1 приведены некоторые характерные значения вязкости. Таблица 1
Коэффициент вязкости жидкости может быть определен методом падающего шарика в вязкой среде (метод Стокса). Рассмотрим свободное падение тела (в нашем случае - свинцового шарика) в вязкой покоящейся жидкости, простирающейся безгранично по всем направлениям. На шарик, свободно падающий в такой жидкости, не оставляющий за собой никаких завихрений (это реализуется при малых скоростях падения шариков малых размеров), действуют три силы: 1. Сила тяжести (P): P = mg = V×r2 ×g = где r - радиус шарика; r2 - плотность шарика; g- ускорение свободного падения; m - масса шарика; V - объем шарика. 2. Выталкивающая сила (сила Архимеда, F1): F1 = Vr1g = где r1 - плотность жидкости. 3. Сила сопротивления движению ( F2, обусловленная силами внутреннего трения между слоями жидкости): F2 = 6 p h r v,(5) где v - скорость слоев жидкости (скорость шарика).
Вначале шарик падает с ускорением и скорость движения шарика возрастает, но по мере увеличения скорости шарика сила сопротивления F2 будет также возрастать и, наконец, наступит такой момент, когда сила тяжести Р будет уравновешена суммой F1 и F2 и ускорение обратится в ноль: P = F1 + F2. (7) С этого момента движение шарика становится равномерным с какой-то скоростью vo. Подставляя в (7) соответствующие значения для Р, F1 и F2, получим для коэффициента вязкости выражение h = Формула (8) справедлива, если шарик падает в жидкости, простирающейся безгранично по всем направлениям. Практически невозможно осуществить падение шарика в безграничной среде, так как жидкость всегда находится в каком-то сосуде, имеющем стенки и определенную высоту столба. Если шарик падает вдоль оси цилиндрического сосуда радиуса R с высотой жидкости h, то учет наличия стенок и высоты дает следующее выражение для h: h =
|

 вязкостью.
вязкостью.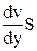 . (1)
. (1)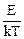 ), (2)
), (2)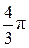 r3×r2×g, (3)
r3×r2×g, (3)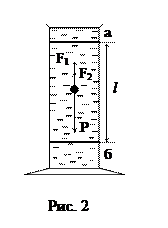 Следует учесть, что здесь играет роль не трение шарика о жидкость, а трение отдельных слоев жидкости друг о друга, поскольку при соприкосновении твердого тела с жидкостью к поверхности тела сразу же прилипают молекулы жидкости. Тело обволакивается слоями жидкости и связано с ними межмолекулярными силами. Непосредственно прилегающий к телу слой жидкости движется вместе с телом со скоростью движения тела. Он увлекает в своем движении соседние слои жидкости, которые на некоторый период времени приходят в плавное безвихревое (ламинарное) движение (если скорость движения мала и диаметр шариков мал). Направление указанных выше сил показано на рис. 2.
Следует учесть, что здесь играет роль не трение шарика о жидкость, а трение отдельных слоев жидкости друг о друга, поскольку при соприкосновении твердого тела с жидкостью к поверхности тела сразу же прилипают молекулы жидкости. Тело обволакивается слоями жидкости и связано с ними межмолекулярными силами. Непосредственно прилегающий к телу слой жидкости движется вместе с телом со скоростью движения тела. Он увлекает в своем движении соседние слои жидкости, которые на некоторый период времени приходят в плавное безвихревое (ламинарное) движение (если скорость движения мала и диаметр шариков мал). Направление указанных выше сил показано на рис. 2.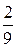 (r2 - r1)
(r2 - r1) 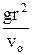 . (8)
. (8)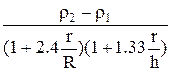 . (9)
. (9)


