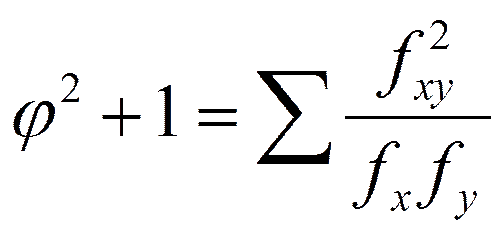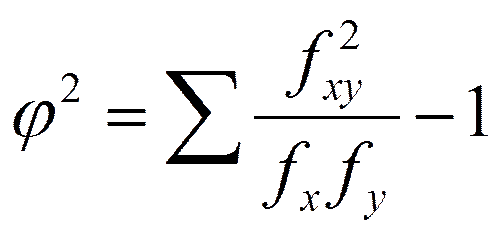Формально статистические методы изучения взаимосвязи.
Понятие и характеристика статистической взаимосвязи.
Изучение взаимосвязей – важнейшая задача статистики. В ее основе - изучение социально-экономической сущности явлений.
Статистические методы изучения взаимосвязи позволяют: 1) выявить наличие и направление связи между признаками; 2) измерить эту связь количественно; 3) выразить связь аналитически (с помощью математической функции).
Связи между явлениями и признаками принято характеризовать по ряду направлений:
1) по роли признаков во взаимосвязи: а) факторные б) результативные
2) по характеру зависимости явлений различают: а) функциональную, т.е. полную; б) корреляционную (неполную) или статистическую связь.
3) по направлению различают прямые и обратные связи.
4) по степени тесноты связи различают сильные (тесные), средние и слабые взаимосвязи.
5) по числу взаимодействующих признаков различают: а) парную связь (парную корреляцию), т.е. связь двух признаков; б) множественную связь (множественную корреляцию), т.е. связь нескольких признаков.
6) по аналитическому выражению различают линейные (прямолинейные) и нелинейные (криволинейные) связи.
7) по опосредованности связи различают: а) непосредственные связи; б) опосредованные (косвенные) связи.
Формально статистические методы изучения взаимосвязи.
Для выявления связи, ее характера и направления пользуются формально статистическими методами анализа. К ним относятся: метод параллельных рядов, балансовый метод, метод аналитических группировок, графический метод.
Графический метод предполагает изображение на плоскости множества пар наблюдений, т.е. X и Y. В результате чего получают поле корреляции, позволяющее по концентрации точек сделать предположение и возможной форме взаимосвязи между факторным и результативным признаком и ее направлением.
Если точки беспорядочно расположены на плоскости, то связь между признаками отсутствует.
Графический метод позволяет построить эмпирическую линию регрессии по данным наблюдения. Для этого определяют средние значения Y и серединное значение Х и эти пары точек наносят на плоскость. Соединив точки, получают ломаную эмпирическую линию регрессии. На основе эмпирической линии регрессии можно определить предполагаемую форму взаимосвязи между признаками.
3. Корреляционно-регрессионный метод изучения взаимосвязи: а) парная корреляция; б) множественная корреляция.
Парная корреляция.
Корреляционно-регрессионный метод анализа позволяет решить 2 задачи: 1)определить аналитическую форму связи между факторным и результативным признаками (между X и Y); 2) установить меру тесноты связи между признаками, т.е. в какой мере вариация факторного признака (X) обуславливает вариацию результативного признака (Y).
y=f(x)
Корреляционно-регрессионный метод анализа включает в себя несколько этапов: 1) постановка задачи и выбор факторных и результативных признаков; 2) изучение взаимосвязей с помощью формально-статистических методов анализа; 3) выбор формы взаимосвязи между факторным и результативным признаком; 4) измерение тесноты взаимосвязи между факторным и результативным признаком; 5) оценка результатов исследования, пояснения и анализ.
Парная корреляция:
1) линейная корреляция имеет место при равномерном изменении признаков.
где a0, a1 – параметры уравнения.
Сущность метода наименьших квадратов состоит в том, что отыскиваются такие значения параметров уравнения регрессии, при которых сумма квадратов отклонений фактических (эмпирических) значений результативного признака от теоретических (вычисленных по функции выравнивания) будет минимальной.
Для нахождения минимума функции приравниваются к нулю частные производные по а0 и по а1.
В результате этого получают систему нормальных уравнений:
где n – число наблюдений (количество пар X и Y) Решая систему уравнений, находят параметры а0 и а1.
2. Если в качестве уравнения связи выбрана парабола второго порядка
3. Если установлено наличие обратной связи между признаками, то функцией связи может являться гипербола
4. Уравнение связи может быть выражено степенной функций:
ПРИМЕР ОПРЕДЕЛЕНИЯ ФУНКЦИИ СВЯЗИ И РАСЧЕТА ПАРАМЕТРОВ УРАВНЕНИЯ СВЯЗИ:
Подставляем значения для нашей задачи:
Логический смысл параметров уравнения линейной регрессии. a0 - показывает усредненное влияние на результативный признак неучтенных факторов. а1 – коэффициент регрессии, показывает, на сколько в среднем изменится значение результативного признака при изменении факторного на единицу.
rxy – линейный коэффициент парной корреляции
Для экономической интерпретации линейных и нелинейных связей пользуются коэффициентом эластичности. Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного на 1%. 1)
2)
Проверка адекватности построенной модели может определяться с помощью средней относительной ошибки аппроксимации:
ε; не должна превышать 12 - 15%.
Множественная корреляция.
Под множественной корреляцией понимается исследование статистической зависимости результативного признака от нескольких факторных признаков.
Линейное уравнение множественной зависимости имеет вид:
где а0, а1, …, ат – параметры функции связи; х1, х2,…, хn- признаки-факторы;
Рассмотрим частные случаи множественной корреляции: а) 2-х факторный комплекс
б) 3-х факторный комплекс
Коэффициенты линейного уравнения множественной регрессии а1, а2,…, аn показывают, на сколько единиц изменится функция с изменением аргумента на 1 единицу при закрепленном положении других аргументов на определенном уровне, обычно среднем. Для интерпретации коэффициентов ai уравнения множественной регрессии используют частные коэффициенты эластичности.
где
ai – коэффициент регрессии при i-ом факторном признаке
Частный коэффициент эластичности показывает, на сколько процентов в среднем изменится функция при изменении аргумента на 1%, при фиксированном значении других аргументов.
4. Показатели тесноты связи:
Параметрические показатели тесноты связи. 1). Линейный коэффициент парной корреляции наиболее точно характеризует тесноту связи при линейной зависимости между факторным и результативным признаком и вычисляется по формуле:
σx – среднее квадратическое отклонение факторного признака
σy - среднее квадратическое отклонение результативного признака
Линейный коэффициент парной корреляции по модулю не превышает 1.
Если
При
Знак выражения «+» - связь прямая. Знак выражения «-» - связь обратная.
2)Эмпирическое корреляционное отношение (рассчитывается по данным наблюдения, т.е. по фактическим данным).
3)Теоретическое корреляционное отношение (индекс корреляции) представляет собой корреляционное отношение, вычисленное на основании результатов выравнивания y по x по некоторой линии.
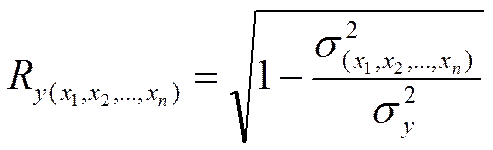
4)Множественный коэффициент корреляции используется для измерения тесноты линейной связи между результативным признаком и двумя или несколькими факторными.
В двухфакторном комплексе коэффициент множественной корреляции рассчитывается по формуле:
где rxz, ryx, ryz – линейные коэффициенты корреляции между признаками.
Для определения тесноты связи между n признаками используются аналогичные формулы:
5)Частные коэффициенты корреляции оценивают степень тесноты связи между двумя признаками при фиксированном значении других признаков(обычно на среднем уровне).
В 2-х факторном комплексе частные коэффициенты корреляции вычисляются по формуле:
Абсолютные величины частных коэффициентов корреляции не могут быть больше абсолютной величины коэффициента множественной корреляции.
Все показатели тесноты связи по модулю не превышают 1. Непараметрические показатели (эмпирические меры) тесноты связи.
1) Коэффициент Фехнера (коэффициент знаков) основан на применении первых степеней отклонений всех значений взаимосвязанных признаков от средней величины по каждому признаку.
а – совпадение знаков отклонений; b – несовпадение знаков отклонений; ∑а – количество совпадений знаков отклонений; ∑b – количество несовпадений знаков отклонений.
Строка (0,+), (0,-),(0,0) не учитывается.
Связь между признаками существенная.
Коэффициент Фехнера позволяет измерить взаимосвязь между двумя количественными признаками. 2) Коэффициент Спирмена (коэффициент корреляции рангов) измеряет тесноту связи между двумя количественными признаками. Для этого определяется ранг каждого элемента.
Ранг – это порядковый номер элемента в ранжированном, т.е. упорядоченном, ряду признаков.
n – число наблюдений.
3) Коэффициент контингенции – это мера тесноты связи двух качественных признаков, состоящих только из двух групп, т.е. альтернативных. ПРИМЕР:
Значения внутри клеток корреляционной таблицы отражают число повторений различных пар наблюдений.
Коэффициент контингенции вычисляется по формуле:
Коэффициент контингенции может иметь знак.
4) Коэффициент ассоциации
Коэффициент контингенции всегда меньше коэффициента ассоциации в силу специфики расчета. Связь считается подтвержденной, если А≥0,5; К≥0,3.
связь между признаками существенная
5) Коэффициент взаимной сопряженности Пирсона – это мера тесноты связи для качественных признаков, каждый из которых состоит более чем из двух групп.
φ2 – показатель взаимной сопряженности
Для исчисления φ2 определяется сумма отношений квадратов частот каждой клетки корреляционной таблицы, изображающей взаимосвязь качественных признаков, к произведению итоговых частот соответствующего столбца и строки.
Вычтя из этой суммы 1, получим φ2
|


 ,
,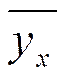 - выровненные или теоретические значения признака,
- выровненные или теоретические значения признака,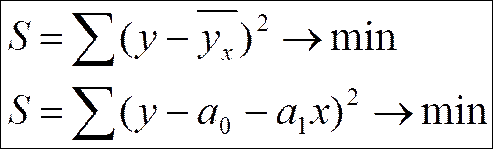
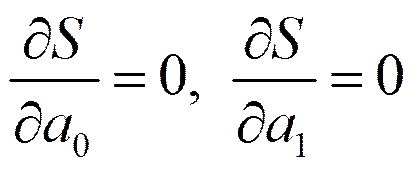
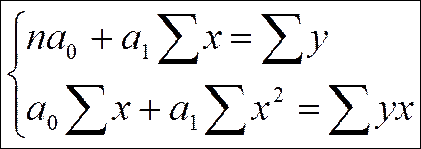 ,
,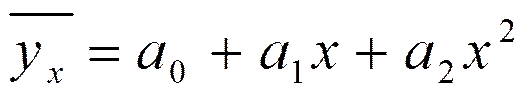
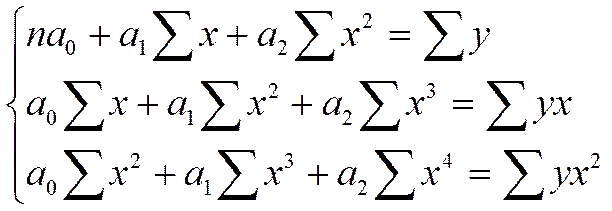


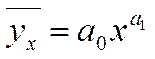
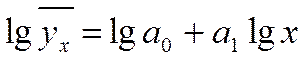



 =47,177
=47,177
 =3,467158
=3,467158
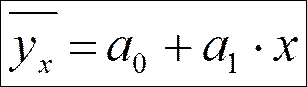





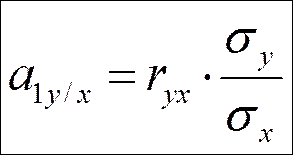 ,
,

 - для линейной зависимости
- для линейной зависимости - для параболы
- для параболы
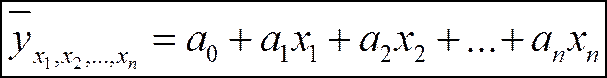
 - выровненные значения результативного признака.
- выровненные значения результативного признака.
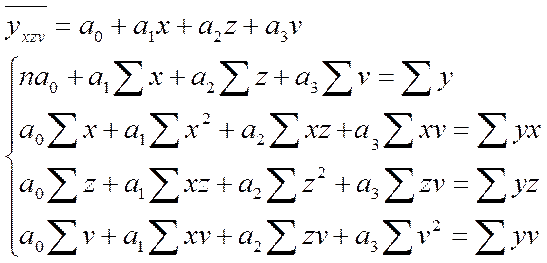

 - среднее значение i-ого факторного признака
- среднее значение i-ого факторного признака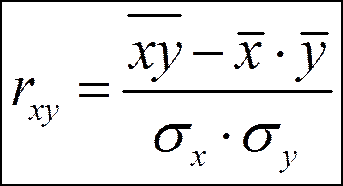
 - средняя величина из произведений значений результативного и факторного признака
- средняя величина из произведений значений результативного и факторного признака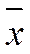 - средняя величина факторного признака
- средняя величина факторного признака - средняя величина результативного признака
- средняя величина результативного признака
 величины независимы.
величины независимы. связь между признаками полная функциональная.
связь между признаками полная функциональная.


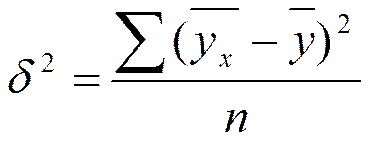
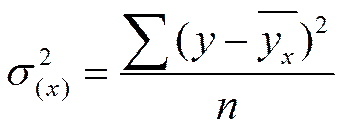

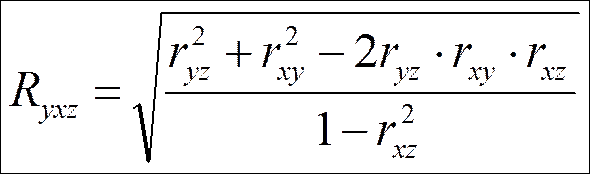

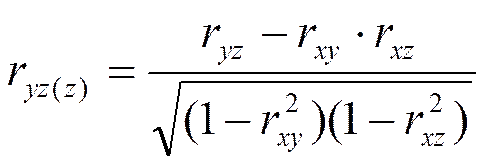


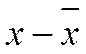
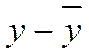


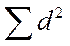 =8
=8

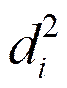 - квадрат разности рангов,
- квадрат разности рангов,
 Высокая
Высокая

 a (25)
a (25)

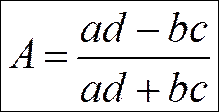
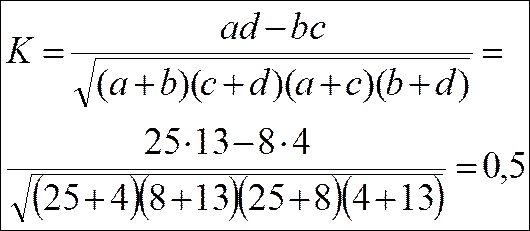

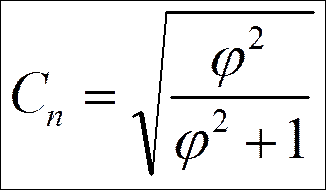
 Квалифика-
ция
зарплата
Квалифика-
ция
зарплата