Связь проницаемости с другими параметрами пористой среды
Зависимость проницаемости от размера пор можно получить с учетом законов Дарси и Пуазейля. Для использования уравнения Пуазейля пористую среду представляют в виде прямых трубок (каналов) одинакового сечения длиной L, равной длине пористой среды. По закону Пуазейля расход жидкости Q через такую пористую среду составит:
где n – число пор приходящихся на единицу площади фильтрации, R – радиус поровых каналов (или средний радиус пор среды), F – площадь фильтрации. Коэффициент пористости:
Однако по закону Дарси
следовательно, Или Величина R, определённая по (1.4.14), характеризует радиус пор идеальной пористой среды, обладающей пористостью m и проницаемостью k. для реальной среды величина R имеет условный смысл, т. к. не учитывает сложного строения и извилистости пор. Можно также воспользоваться формулой Гагена – Пуазейля:
где u – скорость движения жидкости в капилляре (или, что то же, истинная скорость движения флюида в пористой среде), d – диаметр капилляра. Учитывая, что
откуда Котяхов предложил для реальной пористой среды следующую формулу:
где В формулу (1.4.17) введен коэффициент проточности поровых каналов:
Таким образом,
Ряд исследователей выразили проницаемость через другие физические параметры пористой среды: 1. Слихтер (1899) показал влияние упаковки шаров в фиктивном грунте на проницаемость:
где d – диаметр шаров, кS – коэффициент упаковки, зависящий от пористости. 2. Козени (1927) предложил зависимость проницаемости от пористости в виде:
а для несцементированных пород:
где Sуд - удельная поверхность частиц в единице объёма породы. 3. Известна также формула Козени-Кармана:
Из приведенных формул (и из некоторых других) следует, что проницаемость главным образом зависит от размеров пустот. Однако, следует иметь в виду, что в реальных условиях пористость не всегда однозначно определяет проницаемость. Так, глины, например, могут иметь очень высокую пористость – до 50%, однако поры в них, как правило, изолированы и субкапиллярны, а вода находится в связанном состоянии и препятствует продвижению гравитационной воды. Кристаллические породы, наоборот, при низкой пористости (6-8%) могут иметь высокие значения коэффициентов проницаемости за счет вклада проницаемости трещин.
По значениям проницаемости породы делят на три группы: · Проницаемые – породы с коэффициентом проницаемости более 10-2 мкм2. Такие породы характеризуются и значительными коэффициентами пористости (от 20 до 40 %) и сложены такими грубо- и мелкообломочными породами, как гравий, галечники, пески, слабосцементированные песчаники, кавернозные карбонатные и трещиноватые магматические породы. · Полупроницаемые – породы, проницаемость которых находится в пределах от 10-4 до 10-2 мкм2. Это глинистые пески, некоторые песчаники и алевролиты, мелкотрещиноватые известняки и доломиты. Большую часть этих пород занимают субкапиллярные поры. · Практически непроницаемыми считаются породы с коэффициентами проницаемости менее 10-4 мкм2. К таким породам относятся глины, аргиллиты, глинистые сланцы, плотносцементированные песчаники и алевролиты с субкапиллярными порами, плотные карбонатные, магматические и метаморфические породы.
|

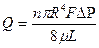 , (1.4.10)
, (1.4.10)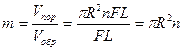
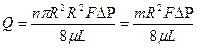 (1.4.11)
(1.4.11) , (1.4.12)
, (1.4.12) и
и  (1.4.13)
(1.4.13)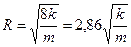 (1.4.14)
(1.4.14) , (1.4.15)
, (1.4.15) , получим:
, получим: ,
, . Или
. Или  , т. е.
, т. е. 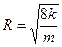 (1.4.16)
(1.4.16) ,
,  (1.4.17)
(1.4.17) - структурный коэффициент,
- структурный коэффициент,  - коэффициент извилистости поровых каналов,
- коэффициент извилистости поровых каналов, 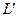 - средняя длина поровых каналов,
- средняя длина поровых каналов,  - прямая, равная длине образца. Величина
- прямая, равная длине образца. Величина  оценивается электрометрическим способом, по скорости движения красителей, ионов и может быть
оценивается электрометрическим способом, по скорости движения красителей, ионов и может быть 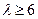 .
.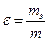 . (1.4.18)
. (1.4.18) . (1.4.19)
. (1.4.19)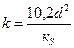 , (1.4.20)
, (1.4.20) , (1.4.21)
, (1.4.21)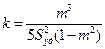 , (1.4.22)
, (1.4.22)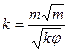 . (1.4.23)
. (1.4.23)


