Принципы построения статистических группировок

При разделении совокупности на группы необходимо решить три основные задачи:

1) определение группировочного признака;

2) определение числа групп;

3) определение величины интервала.

Выбор группировочного признака зависит прежде всего от задач исследования.

Число групп зависит:

- от задач исследования;

- вида признака, положенного в основание группировки;

- численности совокупности;

- степени вариации признака.

Число групп тесно связано с объемом совокупности. Здесь нет строго научных приемов, однако при равенстве интервалов для определения оптимального числа групп может быть использована формула Стерджесса:

n = 1 + 3,322 lgN,

где n –число групп;

N - численность единиц совокупности.

Например, при 200 единицах совокупности число групп определяется следующим образом:

1+3,322 lg200 = 9.

Данной формулой нельзя пользоваться механически. На практике необходимо избегать «пустых» (в которые не попала ни одна единица совокупности) и малочисленных групп.

После определения числа групп решается задача определения интервалов.

Интервал группировки – это интервал значений варьирующего признака, лежащих в пределах определенной группы. Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну из них. Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей – наибольшее значение признака в интервале. Величина интервала - разность между верхней и нижней границами интервала.

Интервалы группировки бывают равные и неравные. Неравные интервалы делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные (и специализированные). Величина интервалов, изменяющихся в арифметической прогрессии, определяется следующим образом:

h _i+1 = h _i + a;

в геометрической прогрессии:

h _i+1 = h _i · q,

где a - константа - число, которое будет положительным при прогрессивно возрастающих интервалах и отрицательным при прогрессивно убывающих интервалах;

q - константа - положительное число, которое при прогрессивно возрастающих интервалах будет больше 1, а при прогрессивно убывающих - меньше 1.

Намечаемые при группировке интервалы бывают открытые (у них указана одна граница: верхняя - у первого, нижняя – у последнего) и закрытые (имеющие нижнюю и верхнюю границы). Необходимость в открытых интервалах обусловлена большой колеблемостью изучаемого признака, разбросом его количественных значений, требующих образования множества групп, если отделять их обеими границами.

Величина равного интервала определяется по следующей формуле:

,

где i – величина интервала;

x_max, x_min – максимальное и минимальное значение признака в совокупности;

n –число групп.

Полученную по формуле величину округляют. Она является шагом интервала. Существуют следующие правила определения шага интервала.

Если величина интервала, рассчитанная по формуле, представляет собой величину, имеющую один знак до запятой (например, 0,66; 1,372; 5,8), то полученные значения целесообразно округлить до десятых и их использовать в качестве шага интервала. В приведенном выше примере шагом интервала будут соответственно значения 0,7; 1,4; 5,8.

Когда рассчитанная величина интервала имеет две значащие цифры до запятой и несколько знаков после запятой, то это значение надо округлить до целого числа. Пусть величина интервала, исчисленная по формуле, равна 12,785. Тогда это значение следует округлить до целого числа, т. е. до 13.

В случае, когда рассчитанная величина интервала представляет собой трехзначное, четырехзначное и так далее число, эту величину необходимо округлить до ближайшего числа, кратного 100 или 50. Например, 248 следует округлить до 250.

При группировке по количественному признаку границы интервалов могут быть обозначены по-разному. Если основанием группировки служит непрерывный признак, то одно и то же значение признака выступает и верхней, и нижней границами у двух смежных интервалов (например, табл. 3). При таком обозначении границ может возникнуть вопрос, в какую группу включать единицы объекта, значения признака у которых совпадают с границами интервалов (например, значение 9 млн. руб.). При ответе на него можно руководствоваться принципом «включительно» верхняя граница или принципом «исключительно». Если в нашем примере (табл. 3) верхняя граница формируется по принципу «включительно», то магазин с объемом продаж 9 млн. руб. необходимо отнести ко второй группе, в противном случае – к третьей. Применение этих принципов зависит от формы написания интервалов, особенно первой и последней групп (употребление слов «свыше», «до», «по», «включительно») или оговаривается отдельно.

Если в основании группировки лежит дискретный признак, то нижняя граница i –го интервала равна верхней границе (i -1)-го интервала, увеличенной на 1.
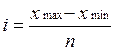