Петренко И.И
Дисциплина «Математика /Высшая математика /Математический анализ
Выполнил(а) студент(ка): Группы ЗАсд-114 Вариан 26 Клементьев М.А. (Ф.И.О.)
Проверил: ст. преподаватель Петренко И.И
Владимир 2015
1. Колинеарны ли векторы С1 и С2, построенные по векторам а и b. а=(2,-1,6). b=(-1,3,8). с1=5а-2b. с2=2а-5b Дано: Найти:колинеарны ли с1 и с2? Решение: с1=(5*2-2*(-1), 5*(-1)-2*3, 5*6-2*8)=(12,-11,14) с2= (2*2-5*(-1), 2*(-1)-5*3, 2*6-5*8)=(9,-17,28) 12=ƛ*9 ƛ=12/9=4/3 -11= ƛ*(-17) ƛ=11/17 14= ƛ*28 ƛ=14/28=1/2 4/3≠11/17≠1/2, нет. 2. Найти косинус угла между векторами
А(3,3,-1) В(5,1,-2) С(4,1,-3) Дано: А(3,3,-1) В(5,1,-2) С(4,1,-3) Найти:Сos( Решение:
Cos( 3. Вычислить площадь параллелограмма,построенного на векторах а и b. а=5p-q, b=p+q, |p|=5, |q|=3, (p^q)=5π/6 Дано: а=5p-q, b=p+q, |p|=5, |q|=3, (p^q)=5π/6 Найти: Sпараллелогр-? Решение: Sпараллелогр=|(5p-q)*(p*q)|=|5p*p+5p*q-q*p-q*q|=|5p*q+p*q)=6|p*q|=6*|p|*|q|*sin(p^q)=6*5*3*1/2=90/2=45(ед2) 4. Компланарны ли вектора а,в и с а=(1,-1,4) в=(1,0,3) с=(1,-3,8) Дано: а=(1,-1,4) в=(1,0,3) с=(1,-3,8) Найти: компланарны ли векторы? Решение: Если вектора компланарны, то |1 -1 4| |1 -1 4| |1 0 3|=0 |1 0 3|=1*0*8+1*(-1)*3+1*(-3)*4-1*0*4-1*(-1)*8-3*(-3)*1=-3-12+8+9=2≠0 |1 -3 8| 1 -3 8| Ответ:не комплонарны. 5. Вычислить объём тетраэдра с вершинами в точках А1,А2,А3,А4 и его высоту опущенную из вершин А4 на грань А1,А2,А3. А1=(0,-3,1) А2(-4,1,2) А3(2,-1,5)А4(3,1,-4) Дано:А1=(0,-3,1) А2(-4,1,2) А3(2,-1,5)А4(3,1,-4) Найти:Vтетр-? h-? Решение:найдём координаты векторов:А1А2=(-4-0,1+3,2-1)=(-4,4,1) А1А3=(2,2,4) А1А4=(3,4,5) |-4 4 1| Объём тетраэдре:V=1/6 | 2 2 4 |=1/6((-4)*2*5+4*4*3+2*4*1-3*2*1-2*4*(-5)-4*4*(-4))=1/6( | 3 4 -5| -80+48+8-6+40+64)=74/6=12
| Sоси=SА1А2А3=А1А2*А1А3= | -4 4 1 |= |2 2 4 | |А1А2*А1А3|= Sоси= Т.к. V=Sоси*h/3 из этого следует h=3V/Sоси=3*74/6*2/ 6. Найдите расстояние от точки М0 плоскости, проходящей через три точки М1,М2,М3 Дано:М1(1,2,0)М2(3,0,-3)М3(5,2,6)М0(-13,-8,16) Найти:расстояние от М0 до пл-ти М1,М2,М3 Решение: Найти ур-ние плоскости: |x-1 y-2 z-0 | |3-1 0-2 -3-0|=0 |5-3 2-2 6-0 | ________________ |x-1 y-2 z | |2 -2 -3 |=(x-1)(-12)+(y-2)(-12)+2*z*0-z*(-8)-12(y-2)-0*(-3)*(x-1)=-12x+12-12Y+24+8z-12y+24= |4 0 6 | =-12x-24y+8z+60=0 Ур-ние плоскости. Расстояние от М0 до пл-ти:d=|(-12)*(-13)+(-24)*(-8)+8*16+60|/ 7. Написать уравнение плоскости, проходящей через точку А перпендекулярно вектору ВС Дано: А(-3,-1,7)В(0,2,-6)С(2,3,-5) Написать уравнение плоскости. Решение ВС=(2,1,1) Уравнение плоскости:2(х+3)+1(y-1)+1(z-7)=0 2x+6+y-1+z-7=0 2x+y+z-2=0
8. Найти угол между плоскостями Дано:2y+z-9=0 x-y+2z-1=0 Найти:y-угол между пл-тями. Решение: Нормальные вектора данных плоскостей: n1=(0;2;1) n2=(1;-1;2) cos y =0*1+2*(-1)+1*2/ y=π/2 Ответ: π/2
9. Найти координаты точки А, равноудалённой от точек В и С Дано: А(х,0,0)- равноудалённый от В(4,5,-2)С(2,3,4) Найти: координаты т.А Решение: АВ= Т.к. по условию АВ=АС, а АС=
Х2-8х+45=х2-4х+29 Х2-8х+45-х2+4х-29=0 -4х+16=0 -4х=-16 Х=4 Т,0 А(4,0,0)
10. Написать канонические уравнения прямой. Дано:х-3y+z+2=0 X+3y+2z+14=0 Написать колонические ур-ия прямой: Решение: колонические ур-ия прямой:
Где (Хо,Yо,Zо) – любая точка прямой S=(m,n,p)-её направляющий вектор. | S=n1*n2=|1 -3 1|=-9 |1 3 2 | Найдём любую точку прямой (Хо, Yo, Zo) Пусть Zo=0, точка
(Хо-3Yo+2=0 (2Xo+16=0 + (Хо+3Yo+14=0 (3Yo=-Xo-14 (XO=- (YO= Т.(-8,-2,0)принадлежит прямой. Кононическое уравнение прямой:
11. Найти точку пересечения прямой и плоскости. Дано: 3Х-2Y+5Z-3=0 Найти:точку пересечения прямой и плоскости. Решение:Запишем параметрические уравнения прямой:
Подставим в ур-ие пл-ти: 3(6t+1)-2(t+3)+5(3t-5)-3=0 18t+3-2t-6+15t-15-3=0 32t-21=0 t= Откуда координаты точки пересечения прямой и плоскости: Х=6* Y= Z=
Ответ:(
|

 а=(2,-1,6). b=(-1,3,8). с1=5а-2b. с2=2а-5b
а=(2,-1,6). b=(-1,3,8). с1=5а-2b. с2=2а-5b и
и 
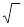 22+(-2)2+(-1)2*
22+(-2)2+(-1)2*  =12
=12 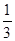 (ед3)
(ед3)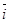
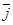
 |
|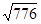
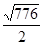
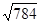 =
=  =19
=19 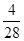 =19
=19 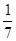
 *
*  =
= 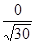 =0
=0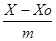 =
= 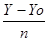 =
= 
 =(-9;1;6)
=(-9;1;6)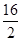 =-8
=-8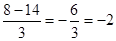
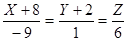
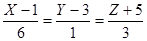
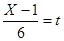 (Х-1=6t (x=6t+1
(Х-1=6t (x=6t+1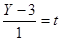 из этого следует (Y-3=t (y=t+3
из этого следует (Y-3=t (y=t+3 (z+5=3t (z=3t-5
(z+5=3t (z=3t-5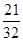
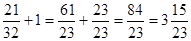


 )
)


