Анализ колебательно-вращательных спектров метана
Колебательно-вращательные спектры молекул являются в своем роде единственным источником полных и надежных данных о внутренних состояниях и физико-химических свойствах молекул. Они несут информацию о строении, внутримолекулярной динамике и об электрооптических свойствах молекулы, которые широко используются в задачах взаимодействия излучения с веществом. Извлечение такой информации из высокоточных экспериментальных спектров является одной из фундаментальных задач молекулярной спектроскопии. Решение этой проблемы разбивается, как правило, на два этапа. Первый этап представляет собой теоретическое моделирование, позволяющее с помощью спектроскопических параметров моделей описывать спектр молекулы с экспериментальной точностью. Одной из особенностей этого этапа является исключительно высокая точность регистрации экспериментальных спектров, что требует, в свою очередь, высокой точности расчетов и адекватности моделей. Второй, более сложный, этап исследований в рамках указанной проблемы заключается в извлечении информации о фундаментальных характеристиках молекулы из найденных спектроскопических параметров моделей. Это предполагает установление аналитических зависимостей спектроскопических параметров от молекулярных постоянных. Наиболее широко распространенным при расчете колебательно-вращательных спектров является метод эффективных операторов – эффективного гамильтониана и эффективного дипольного момента. Эффективные операторы служат не только инструментом прямого расчета спектра молекулы, но и задают математические модели, которые применяются при обработке экспериментальных данных. Основным преимуществом этого метода является возможность лимитировать расчет некоторой локализованной группой близко расположенных колебательных состояний, представляющих интерес для конкретного эксперимента. Наряду с научной значимостью спектроскопических исследований на передний план выносится разработка техники и методики проведения качественного и количественного анализа молекулярных сред. Примером являются газовые анализаторы, которые широко используются в экологии, в горнодобывающей промышленности, в геодезии и т.д. Принцип работы газоанализаторов основан на регистрации колебательных спектров различных молекулярных газов. Проанализируем строение и колебательно-вращательные спектры молекулы метана CH4 . Центральный атом углерода в основном состоянии характеризуется электронной конфигурацией
Для анализа экспериментальных колебательных спектров метана необходимо произвести теоретико-групповой анализ колебаний этой молекулы. Задачами этого анализа является установление симметрии колебаний молекулы и определение активности различных колебательных частот в ИК спектре поглощения и в КР спектре. Молекула
Таблица 1 – Типы симметрии для группы
Общее число (с учетом трансляций и вращений) колебаний
где h – число операций симметрии в рассматриваемой группе симметрии (порядок группы), hi – число операций симметрии в i -ом классе (эквивалентные преобразования симметрии объединяются в один класс),
Суммирование ведется по всем классам (при hi =1 – по всем операциям симметрии). Характеры приводимых представлений
(p =1, … n -1) Здесь Истинное число колебаний s - го типа симметрии определяется по формуле
где Далее определяется активность колебаний в ИК и КР спектрах: - колебание s - го типа симметрии активно (проявится) в ИК спектре поглощения, если этому же типу симметрии соответствует(ют) трансляции Т (или координатные составляющие дипольного момента - колебание s - го типа симметрии активно в КР спектре, если этому же типу симметрии соответствует(ют) матричные элементы тензора поляризуемости ( Определение типов симметрии колебаний молекулы существенно упрощает колебательную задачу, поскольку колебания определенного типа симметрии следует рассматривать независимо от остальных колебаний. Используя полученную о типах симметрии колебаний информацию, представляется возможным проводить анализ экспериментальных колебательных спектров рассматриваемой молекулы. На рисунках 4 и 5 представлены колебательно-вращательные полосы основного тона и первого обертона трехкратно вырожденного антисимметричного валентного колебания молекулы метана. Анализируя эти спектры, можно определить: 1. Параметры антисимметричного валентного колебания, каковыми являются собственная частота
Здесь
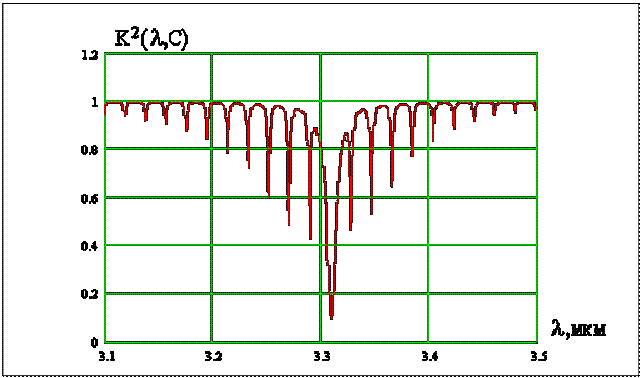
2. Межъядерное расстояние В общем случае к геометрическим параметрам молекул относятся равновесные расстояния между атомами (межъядерные расстояния) в молекуле и углы между связями. Эти параметры представляют собой вполне определенные величины и отвечают условиям, при которых силы притяжения между ядрами уравновешиваются силами отталкивания. Для экспериментального определения молекулярных констант необходимо найти значения моментов инерции, которые связаны с вращательными постоянными молекулы. Вращательную же постоянную можно найти из анализа колебательно-вращательного спектра поглощения по величине разности волновых чисел соседних максимумов поглощения. Молекула метана, как следует из таблицы 1, характеризуется восемью осями третьего порядка и относится к разряду групп высшей симметрии. Вращение таких молекул описывается в рамках модели сферического волчка для которого моменты инерции вращений относительно трех главных осей одинаковы. Для определения межъядерного расстояния r связи C–H удобно выбрать ось вращения, проходящую через центры атома углерода и одного из атомов водорода (ось Z). Тогда момент инерции будет равен
где l – проекция межъядерного расстояния r на основание тетраэдра, Момент инерции молекулы связан с ее вращательной постоянной В формулой
Значение вращательной постоянной B (м-1) находят, определив волновые числа колебательно-вращательных пиков в спектре поглощения метана. Если влияние колебательного движения на вращение молекулы пренебрежимо мало, для волнового числа линий P - и R - ветвей колебательно вращательной полосы можно воспользоваться формулами
Здесь Если колебательно-вращательные компоненты полосы расположены в шкале волновых чисел неравномерно, то следует учитывать колебательно-вращательное взаимодействие, при котором волновые числа определяются формулами
Здесь
Вопросы для самоконтроля знаний
1 В чем состоит явление гибридизации атомных орбиталей? 2 Чем обусловлена тетраэдрическая структура молекулы метана? 3 Из каких элементов симметрии состоит группа 4 Какие типы симметрии (неприводимые представления) соответствуют группе 5 Как определить число нормальных колебаний молекулы, характеризующихся определенным типом симметрии? 6 Как определить активность нормального колебания в ИК и КР спектрах? 7 Сколько различающихся по величине моментов инерции соответствуют вращению молекулы метана? 8 Какой формулой в рамках модели жесткого ротатора определяются волновые числа колебательно-вращательных переходов? 9 Каким образом в колебательно-вращательном спектре проявляется влияние колебательного движения молекулы на ее вращение?
|

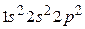 . Поскольку энергии 2s - и 2p -электронов мало отличаются, образование химических связей атома углерода с другими атомами осуществляется посредством всех четырех электронов
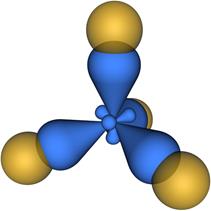
. Поскольку энергии 2s - и 2p -электронов мало отличаются, образование химических связей атома углерода с другими атомами осуществляется посредством всех четырех электронов  Распределение электронной плотности, соответствующее совокупности этих электронов (гибридизации), является определяющим фактором при формировании химических связей. На рисунке 1 схематически показано образование гибридных атомных орбиталей при
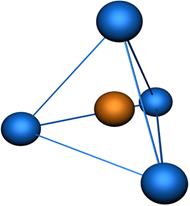
Распределение электронной плотности, соответствующее совокупности этих электронов (гибридизации), является определяющим фактором при формировании химических связей. На рисунке 1 схематически показано образование гибридных атомных орбиталей при 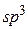 - гибридизации, реализующейся в молекуле метана. Распределение электронной плотности при образовании химической связи между атомом углерода и четырьмя атомами водорода в молекуле метана схематически показано на рисунке 2. Указанная особенность образования химических связей в молекуле метана проявляется в том, что эта молекула в равновесном состоянии имеет форму тетраэдра (рис 3), что соответствует точечной группе симметрии
- гибридизации, реализующейся в молекуле метана. Распределение электронной плотности при образовании химической связи между атомом углерода и четырьмя атомами водорода в молекуле метана схематически показано на рисунке 2. Указанная особенность образования химических связей в молекуле метана проявляется в том, что эта молекула в равновесном состоянии имеет форму тетраэдра (рис 3), что соответствует точечной группе симметрии  (таблица 1).
(таблица 1).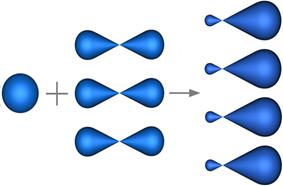

 характеризуется
характеризуется 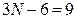 колебаний. Для того, чтобы определить симметрию всех колебаний, необходимо воспользоваться таблицей типов симметрии
колебаний. Для того, чтобы определить симметрию всех колебаний, необходимо воспользоваться таблицей типов симметрии 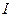
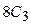
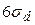
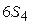
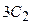
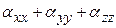

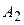
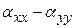 ,
, 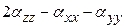
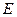
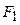
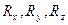
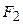
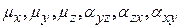
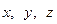
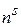 , соответствующих типу симметрии s, определяется по формуле
, соответствующих типу симметрии s, определяется по формуле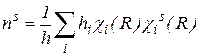 (1)
(1)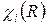 – характер приводимого представления в i -ом классе для операции симметрии R,
– характер приводимого представления в i -ом классе для операции симметрии R, – характер неприводимого представления в i- ом классе для операции симметрии R (определяется из таблицы типов симметрии рассматриваемой группы).
– характер неприводимого представления в i- ом классе для операции симметрии R (определяется из таблицы типов симметрии рассматриваемой группы).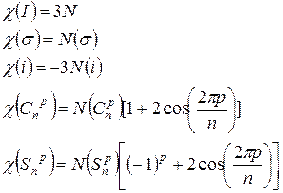 (2)
(2) ,
, 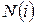 ,
,  ,
, 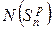 – число атомов, не меняющих своего положения при выполнении соответствующей операции симметрии.
– число атомов, не меняющих своего положения при выполнении соответствующей операции симметрии.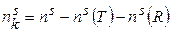 , (3)
, (3)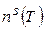 ,
,  - число трансляций и вращений, характеризующихся типом симметрии s (определяется из таблицы 1).
- число трансляций и вращений, характеризующихся типом симметрии s (определяется из таблицы 1).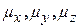 );
);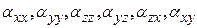 ).
).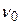 и параметр ангармоничности
и параметр ангармоничности 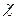 . Для определения значений этих величин следует воспользоваться формулой для частот колебательного спектра
. Для определения значений этих величин следует воспользоваться формулой для частот колебательного спектра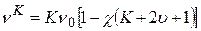 . (4)
. (4)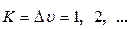 для основного тона, первого обертона и т.д.,
для основного тона, первого обертона и т.д.,  - колебательное квантовое число энергического уровня, с которого происходят поглощательные переходы молекул.
- колебательное квантовое число энергического уровня, с которого происходят поглощательные переходы молекул.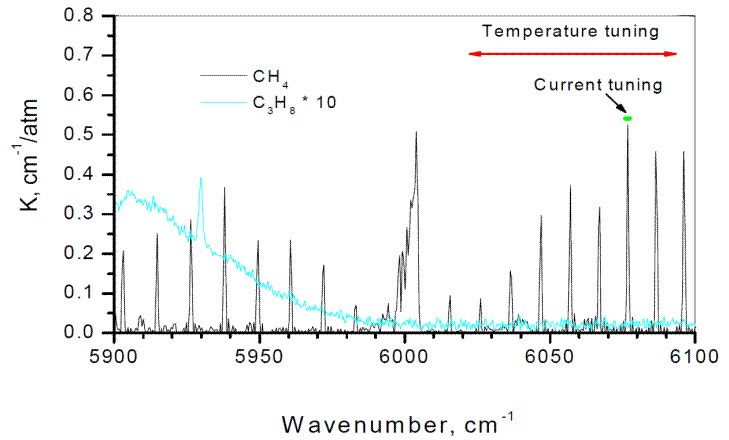
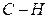 в молекулы метана.
в молекулы метана. , (5)
, (5)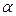 - угол, смежный
- угол, смежный  , т.е.
, т.е.  .
.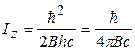 , (6)
, (6)
 , (7)
, (7)
 . (8)
. (8)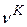 - частота чисто колебательного перехода, значение которой определяется в соответствии с формулой (4).
- частота чисто колебательного перехода, значение которой определяется в соответствии с формулой (4).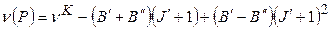 ,
, 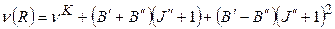 ,
, 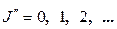 (10)
(10)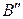 ,
, 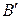 - вращательные постоянные нижнего и верхнего колебательных состояний, соответственно.
- вращательные постоянные нижнего и верхнего колебательных состояний, соответственно.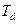 ?
?


