Позиционные системы счисления
Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов (цифр), необходимых для записи любых чисел. Основанием позиционной системы счисления называется возводимое в степень целое число, котороеравно количеству цифр, используемых для изображения чисел в данной системе счисления. Основание показывает также, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию. Возможно множество позиционных систем, так как за основание системы счисления можно принять любое число не меньшее 2. Наименование системы счисления соответствует ее основанию (десятичная, двоичная, восьмеричная, шестнадцатеричная и т. д.).
Десятичная система характеризуется тем, что в ней 10 единиц какого-либо разряда образуют единицу следующего старшего разряда. В системе счисления с основанием q (q-ичная система счисления) единицами разрядов служат последовательные степени числа q. Для записи чисел в q-ичной системе счисления требуется q различных цифр (0,1,...,q-1). В позиционной системе счисления любое вещественное число в развернутой форме может быть представлено в следующем виде:
или
Здесь А — само число, q — основание системы счисления, ai —цифры, принадлежащие алфавиту данной системы счисления, n — число целых разрядов числа, m — число дробных разрядов числа.
Свернутой формой записи числа называется запись в виде
13. Как переводятся числа из различных СС в 10-ую СС
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики: При переводе удобно пользоваться таблицей степеней двойки: Таблица 4. Степени числа 2
Пример. Число 2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики: При переводе удобно пользоваться таблицей степеней восьмерки: Таблица 5. Степени числа 8
Пример. Число 3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики: При переводе удобно пользоваться таблицей степеней числа 16: Таблица 6. Степени числа 16
Пример. Число
14. Что понимается в системах счисления под «триадой» и «тетрадой» когда она может применяться. Восьмеричная система счисления. Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада).
Аналогично с 16-тиричной СС: Шестнадцатеричная система счисления. Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр – латинскими буквами: 10–A, 11–B, 12–C, 13–D, 14–E, 15–F. Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада).
16.Нормализованная форма. Форма представления числа с плавающей точкой, при которой мантисса М (Мантисса — дробная часть логарифма числа.) удовлетворяет двум условиям: М<1 и старшая цифра мантиссы отлична от нуля. Представляется в последовательности общего числа разрядов: знак, мантисса, знак порядка, порядок. Пример: 0,584*102 –нормализованное число. (0,0457*103-ненормализованное число.) 0,9876*102=0,9876+2=0,9876Е+2. Преимущества: 1. Большой диапазон представления чисел. 2.Не требует масштабирования исходных данных. Недостатки: Меньше производительность. 17. Дизъюнкция - логическое сложение, логическое ИЛИ. Истина, тогда, когда хотя бы 1 истина
18. Конъюнкция – логическое умножение, логическое И, истина, когда оба истина.
|

 aiqi
aiqi


 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
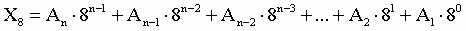

 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.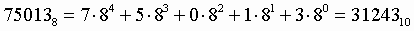
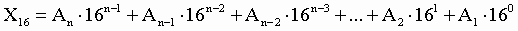
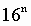
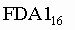 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.


