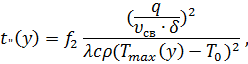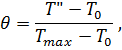Расчетное определение термических циклов в точках ЗТВ
Для автоматической сварки под флюсом характерны большие эффективные тепловые мощности дуги и высокие скорости сварки. По мере увеличения скорости сварки при пропорциональном наращивании выделяемой в дуге мощности, когда q→:, υсв →:, q/ υсв =const, длина изотерм увеличивается пропорционально скорости сварки, а их ширина возрастает, стремясь к определенному пределу. Нагретая область при этом располагается узкой полосой вдоль пути перемещения дуги – изотермы в основной их части практически параллельны оси шва. На этом основании делается допущение, что теплота распространяется преимущественно в направлении, перпендикулярном к оси шва, а распространение теплоты вдоль оси пренебрежимо мало. Это допущение, оправданное для мощных быстро движущихся источников теплоты, сводит действительную двумерную тепловую задачу, характерную для пластин, к одномерной. Следует отметить, что это допущение приемлемо в основном только для автоматической сварки материалов с низкой теплопроводностью (малоуглеродистые, низкоуглеродистые и нержавеющие стали, титановые сплавы и т.п.). Рассмотрим схематично решение этой задачи, впервые полученное основоположником теории распространения теплоты при сварке академиком Н.Н.Рыкалиным.
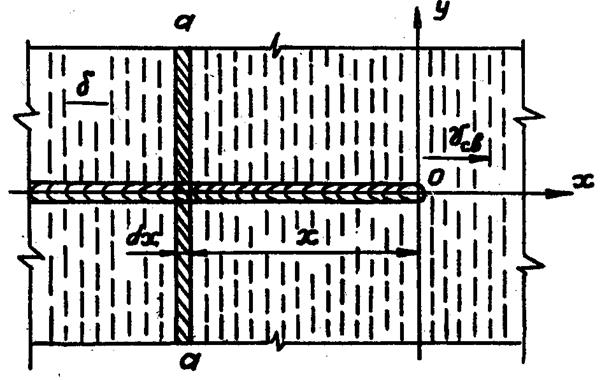
Рис. 5. Схема разбиения пластины на элементарные стержни сечением F=δdx.
Пусть в неограниченной пластине толщиной δ в направлении оси Ох (рис. 5) перемещается равномерно и прямолинейно мощный быстро движущийся линейный источник теплоты: q=const, υсв =const. На основании сделанного допущения полагаем, что теплота, введенная источником в пластину, распространяется только в направлении оси Оу. Разделим пластину сечениями, перпендикулярными к оси перемещения источника, на бесконечное количество полосок (стержней) с поперечным сечением F=δ*dx. Рассмотрим стержень a-a, находящийся на расстоянии X позади источника теплоты. Этому стержню при прохождении через него линейного источника было сообщено мгновенное количество теплоты, равное dQ=q*dt=(q*dx)/ υсв. Вследствие теплопроводности материала теплота распространяется в направлении оси как от действия плоского источника (перетекания теплоты в соседние стержни не происходит). Время распространения теплоты в рассматриваемом стержне равно t =x/ υсв (отсчет времени начинается с момента пересечения источником теплоты рассматриваемого стержня). Процессы, происходящие в других стержнях, аналогичны рассмотренному и отличаются только временем начала действия мгновенного источника теплоты. Таким образом, при принятом допущении распространение теплоты дуги в пластине описывается схемой плоского источника. Из общей теории теплопроводности для случая действия мгновенного плоского источника теплоты в неограниченном стержне процесс изменения температуры определяется уравнением:
Подставив в выражение (1) интенсивность мгновенного плоского источника, которая в рассматриваемом случае равна:
и введя коэффициент
Заметим, что для толщин δ >3..4 мм теплоотдачей можно пренебречь, т.е. принять b=0. Выражение (2) является уравнением предельного состояния процесса распространения теплоты при нагреве пластаны мощным быстро движущимся линейным источником теплоты. Уравнение позволяет рассчитать термические циклы в интересующих нас точках сварного соединения. Из выражения (2) также можно получить формулы для расчета важных характеристик термического цикла: 1. Выражение для определения кривой максимальных температур - совокупности максимальных значений температур в отдельных точках Tmax=f(y):
2. Выражение для определения мгновенных скоростей охлаждения металла шва (y=0) при различных его температурах W=f(T):
При небольших температурах Т формула (4) позволяет вычислять мгновенные скорости охлаждения достаточно точно и для точек ЗТВ (y > 0). 3. Длительность нагрева t„ выше температуры Т”:
где f2 - табулированная функция величины θ:
Величина t,, может быть определена более просто непосредственно ив графика термического цикла конкретной точки.
|


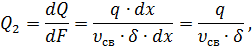
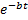 , учитывающий теплоотдачу боковых поверхностей пластины в воздух, окончательно получим:
, учитывающий теплоотдачу боковых поверхностей пластины в воздух, окончательно получим: