ПОГРЕШНОСТЬ ИЗМЕРЕНИЙ
В силу статистического характера процесса радиоактивного распада из- меряемая величина (число отсчетов за фиксированное время экспозиции) при многократном повторении испытывает колебания около наиболее ве- роятного значения. Поэтому, если в стандартных условиях (постоянство экспозиции и эффективности регистрации) имеем k результатов измерения долгоживущей активности, то их распределение будет следовать распреде- лению Пуассона, которое имеет следующие характерные свойства – резкую ассиметричность (при малом числе отсчетов), целочисленность и неотрица- тельность значений. Наилучшее приближение к истинному значению дает среднее, рассчитываемое из соотношения
Это обстоятельство позволяет проводить проверку гипотезы о подчи- нении эмпирического распределения закону Пуассона
для Ni= 0, 1, 2….. При достаточно большом значении
Эта запись означает, что с доверительной вероятностью 68% истинное зна- чение числа отсчетов лежит в указанном интервале. Относительная пог- решность измерения равна
С другой стороны, для расчетов результат радиометрической реги- страции удобнее выразить через скорость счета Этот подход не рационален, когда нет других источников погреш- ности, поскольку существенно увеличивает трудоемкость измерений, не давая никакого улучшения точности. Но если процесс измерения вы- полняется под управлением микроэвм по соответствующей программе, то эта проблема снимается. Массив данных параллельных определений, полу- ченных по установленному регламенту, позволяет проводить проверку различных статистических гипотез, например, о вкладе других источников слу- чайной погрешности или наличии систематического смещения результатов. Оценка точности измерения сигнала при наличии фона прибора. В реальных условиях скорость счета сигнала nс равна n с = n пр - n ф, где n ф– скорость счета фона, а n пр – скорость счета препарата (сигнал + фон). Поскольку при суммировании или вычитании случайных величин их дисперсии складываются, то для скорости счета сигнала имеем ơс2 = ơпр2 + ơф2. Если время измерения препарата и фона было различным, то стандартное отклонение сигнала составит
Соответственно, относительная погрешность равна
Измерения в случае хорошо известного фона. Фон прибора при устойчивой работе, отсутствии внешних воздействий и внутренних заг- рязнений постоянен и может быть определен с высокой точностью, пос- кольку измерения фона проводятся неоднократно. Это означает, что обеспечивается условие n пр /t пр >>n ф /t ф. Тогда относительная погреш- ность результата при достаточно высокой скорости счета определяется только условиями измерения препарата
Уравнение 3 позволяет определить длительность измерения с заданной относительной точностью. Оно применимо и в случае n пр >>n ф, что рав- носильно n с ~ n пр. Оптимальный режим измерения, когда фон заранее не известен. Измерение слабоактивных препаратов часто приходится проводить, когда фон не был установлен в предварительных экспериментах. Тогда для по- лучения результата с заданной точностью при минимальных затратах вре- мени на измерения требуется правильно установить экспозицию фона (t ф) и препарата (t пр), соотношение между которыми зависит от величины n пр и n ф. Эта задача решается путем определения минимума δс в уравнении 2, учи- тывая при этом, что полное время измерения ограничено и равно T = t пр + t ф. В конечном итоге получаем
Из уравнений 2 и 4 следует
Длительность измерения фона определяется по уравнению 4. Для установления оптимального режима регистрации по уравнениям 4 и 5 требуется предварительная оценка величин n пр и n ф в ходе кратковре- менных измерений. Оценка чувствительности радиометрической установки. Важную характеристику радиометрической установки представляет уровень мини- мальной регистрируемой активности. Он задает предел обнаружения в ак- тивационном анализе, определяет возможность изучения ядерных реакций с низким сечением и регистрации слабоактивных препаратов. За минимальную принимают такую скорость счета, которую за время t пр можно установить с относительной погрешностью δ. Последнюю обыч- но принимают равной 0,2. Соответствующее выражение для установки с постоянным фоном выводится на основе уравнения 3
Известная эффективность счета позволяет перейти к минимальной опреде- ляемой активности
Таким образом, минимальная регистрируемая активность определяется как параметрами радиометра (n ф, εрег), так и условиями измерения (δ, t пр). Наиболее высокую чувствительность (минимальную регистрируемую ак- тивность) имеют специальные высокоэффективные установки с 4π-геомет- рией (εрег~1) и системой антисовпадений для подавления космического из- лучения (n ф ~ 0,1 отсчет/мин). Оценка стабильности работы радиометрической установки. Для получения надежных данных необходим контроль работы радиомет- рической установки. Для этого периодически измеряют фон, а также долго- живущий радиоактивный препарат. Контроль фона позволяет своевремен- но выявлять загрязнение системы, воздействие внешних помех, неустой- чивость работы детектора. Измерения эталонного препарата в строго фик- сированных условиях (постоянство εрег и t пр) демонстрируют стабиль- ность работы установки, на которую могут влиять колебания в электро- питании, температура среды, старение детектора и т.д. Набор данных, полученных при этом, позволяет вычислить выбо- рочную дисперсию по уравнению
Дисперсия, которая должна быть при стабильной работе радиометра, т. е. при следовании распределению Пуассона, равна Выявление систематического смещения средних месячных результатов проводится с применением критерия Стьюдента. В радиометрической практике довольно распространена ситуация, когда искомая величина не фиксируется непосредственно в эксперименте, а полу- чается в результате расчета по заданному соотношению измеренных параметров. Простейший пример – относительные измерения, когда содер- жание искомого компонента рассчитывается по соотношению
где параметр m представляет содержание определяемого компонента, а па- раметр n – скорость счета; индексы x и этобозначают принадлежность указанных параметров соответственно к исследуемой пробе и эталону. При строгом постоянстве эффективности регистрации излучения аналитическо- го радионуклида, обеспечения точного значения m эт и отсутствии помех от других источников погрешность конечного результата (mx) будет зависеть только от статистики зарегистрированной радиоактивности пробы и этало- на (nx, n эт). Относительная погрешность результата косвенного измерения рассчитывается по соотношению
где Указанный подход к оценке относительной погрешности конечного ре- зультата следует применять при выполнении некоторых последующих за- даний данного практикума. В заключение следует отметить, что в исследованиях, связанных с ре- гистрацией ионизирующего излучения, статистика числа отсчетов пред- ставляет собой только один из возможных источников погрешности. Полу- чение надежных и точных результатов требует учета всех факторов, кото- рые могут влиять на конечный результат. А методика исследования должна предусматривать снижение вклада любого источника погрешности до ми- нимального уровня.
|

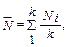 где Ni – выборочное значение результата, k – число измерений. Из выше- сказанного следует, что результат радиометрической регистрации всегда имеет некоторую неопределенность, мерой которой является, как это при- нято, стандартное отклонение (среднеквадратическая погрешность). Осо- бенностью полученного массива данных является то, что среднее ариф- метическое и диcперсия равны между собой
где Ni – выборочное значение результата, k – число измерений. Из выше- сказанного следует, что результат радиометрической регистрации всегда имеет некоторую неопределенность, мерой которой является, как это при- нято, стандартное отклонение (среднеквадратическая погрешность). Осо- бенностью полученного массива данных является то, что среднее ариф- метическое и диcперсия равны между собой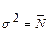 ,
,
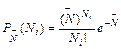
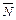 (³25) распределение Пуассона хорошо аппроксимируется распределением Гаусса,
(³25) распределение Пуассона хорошо аппроксимируется распределением Гаусса,  . Этот переход очень важен, так как позволяет делать оценку погреш- ности радиометрического определения в рамках хорошо освоенной статистики Гаусса. Тогда доверительный интервал для измеряемой величины будет иметь вид:
. Этот переход очень важен, так как позволяет делать оценку погреш- ности радиометрического определения в рамках хорошо освоенной статистики Гаусса. Тогда доверительный интервал для измеряемой величины будет иметь вид: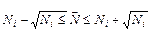
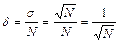
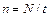 . Доверительный интервал в этом случае равен
. Доверительный интервал в этом случае равен 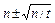 . Отсюда следует, что погрешность скорости счета падает с увеличением длительности измерения пропор- ционально
. Отсюда следует, что погрешность скорости счета падает с увеличением длительности измерения пропор- ционально 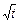 . Иными словами, чтобы обеспечить заданную точность ре- зультата, надо правильно установить длительность однократного изме- рения. Иногда в этих целях прибегают к параллельным определениям с последующей оценкой точности методами статистики Гаусса.
. Иными словами, чтобы обеспечить заданную точность ре- зультата, надо правильно установить длительность однократного изме- рения. Иногда в этих целях прибегают к параллельным определениям с последующей оценкой точности методами статистики Гаусса.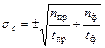 (1)
(1)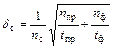 (2)
(2)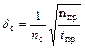 (3)
(3)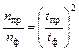 (4)
(4)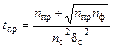 (5)
(5)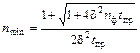 (6)
(6)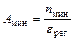 (7)
(7)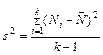 (8)
(8)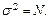 Отношение дис- персий сравнивается с F- критерием, значение которого для принятого уровня надежности (обычно 0,05) и числе степеней свободы f = k – 1 бе- рут из таблиц по статистике. Если соблюдается условие s2/σ2 ≤ F0.05 (f, ∞), то с вероятностью 95% гипотезу о нестабильности установки следует от- клонить. В противном случае действительна альтернативная гипотеза. Для надежности оценок к должно быть достаточно велико (к >; 11). Критерий Фишера служит для проверки гипотезы о появлении дополнительного ис- точника случайной погрешности.
Отношение дис- персий сравнивается с F- критерием, значение которого для принятого уровня надежности (обычно 0,05) и числе степеней свободы f = k – 1 бе- рут из таблиц по статистике. Если соблюдается условие s2/σ2 ≤ F0.05 (f, ∞), то с вероятностью 95% гипотезу о нестабильности установки следует от- клонить. В противном случае действительна альтернативная гипотеза. Для надежности оценок к должно быть достаточно велико (к >; 11). Критерий Фишера служит для проверки гипотезы о появлении дополнительного ис- точника случайной погрешности.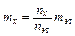 ,
,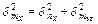
 и
и 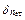 − соответственно относительная погрешность скорости счета радионуклида в пробе и эталоне.
− соответственно относительная погрешность скорости счета радионуклида в пробе и эталоне.


