ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКА ИЗМЕРЕНИЙ
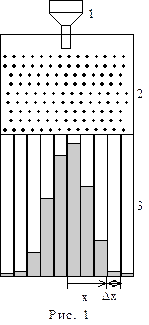
Установка, на которой моделируется распределение молекул по скоростям, схематически изображена на рис. 1 и носит название доски Гальтона.
Поток мелких частиц (горох или силикагель) высыпается из воронки 1и рассеивается на вбитых в доску гвоздях 2. Рассеянные частицы попадают затем в ячейки накопителя 3. Эти ячейки имеют одинаковую ширину Dx, поэтому о числе частиц, попадающих в них, можно судить по высоте уровня, до которого та или иная ячейка заполнена частицами. Измеряя эти высоты, мы можем найти вероятность попадания в них частиц. Эта вероятность Р(x), благодаря случайному характеру рассеяния частиц, зависит от расстояния x, на которое отклонились частицы в горизонтальном направлении от середины доски, по закону Гаусса[1]:
Здесь Ро и s - const, Dx – ширина ячейки накопителя. Поскольку расстояние x можно записать в виде: x= где
мы вместо (1) получим:
то есть распределение Максвелла. Итак, изучая рассеяние частиц по доске Гальтона, мы, тем самым, изучаем распределение этих частиц по скоростям, которое имеет вид распределения Максвелла. Величина скорости
Учитывая, что распределение Максвелла (4) можно записать также в виде:
мы видим, что в данной установке, согласно (5) и (6) «температура» потока частиц определяется расстоянием между гвоздями: T~R2 (7). Поскольку цель работы состоит в проверке соотношения (1), то для удобства проверки следует несколько преобразовать это соотношение, для чего прологарифмируем его:
Поскольку х можно записать в виде: x = i×Dx (9) где i – номер соответствующей ячейки (нумерация идет от середины доски), то (8) примет вид:
где введены обозначения: Pi = DP(i×Dx), B= ln(Po×Dx). Из (10) видно, что если соотношение (1) справедливо, то зависимость lnPi от i2 носит линейный характер. Кроме того, как видно из (10), k– угловой коэффициент наклона графика к оси х равен:
Поэтому для двух разных досок отношение величины s1/s2 равно корню квадратному из отношения соответствующих коэффициентов наклона:
А поскольку, согласно определению
то
Отношение же «температур» потоков:
|

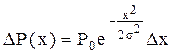 (1).
(1).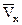 t (2),
t (2),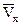 – средняя скорость частиц, попавших в ячейку на расстояние х от середины доски, t – среднее время движения частиц по доске, то, обозначая:
– средняя скорость частиц, попавших в ячейку на расстояние х от середины доски, t – среднее время движения частиц по доске, то, обозначая: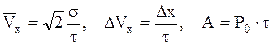
 (3),
(3),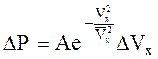 (4),
(4),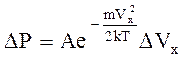 (6)
(6)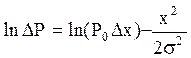 (8)
(8)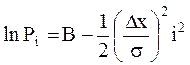 (10)
(10)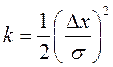 (11).
(11).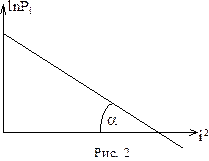
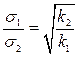 (12)
(12)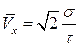 (13)
(13)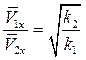 (14)
(14)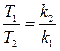 (15).
(15).


