Ошибки округления
Даже, если предположить, что исходная информация не содержит никаких ошибок, а все вычислительные процессы конечны, то все равно и в этом случае присутствует третий тип ошибок - ошибки округления. Предположим, что вычисления производятся на машине, в которой каждое число может представляться не более, чем пятью значащими цифрами (отличать от термина “пять знаков после запятой“), например, 15735, 23.749, 0.16783, 0.000093436. Пусть необходимо сложить два числа 9.2654 и 7.1625, причем эти два числа являются точными. Точное значение этой суммы равно 16.4279, но оно содержит 6 значащих цифр и потому не помещается в разрядной сетке нашей гипотетической машины. Поэтому результат будет округлен до 16.428 и при этом возникнет ошибка округления. Так как ЭВМ всегда работает с конечным количеством значащих цифр, то округление результатов арифметических операций производится очень часто. Для изучения округления действительных чисел необходимо рассмотреть форму представления таких чисел в памяти ЭВМ. Для представления вещественных чисел используется так называемая форма “с плавающей точкой”, в которой число записывается через мантиссу и порядок 56.73.10-1, или 5.673.101, или 0.5673.102, или 0.05673.103 и т.д., т.е. для одного и того же числа можно записать много форм его представления с плавающей точкой. Среди всех этих представлений есть одно, особенное, называемое нормализованным. Для нормализованного представления выполняется: 0,1 т.е. целая часть мантиссы равна нулю, а дробная часть в старшем разряде содержит любую цифру кроме нуля. Рассмотрим процесс сложения двух чисел А=162.45 и В=1.7698 в нашей гипотетической 5-разрядной ЭВМ. В нормализованном представлении с плавающей точкой А=0.16245.103, В=0,17698.101. Сначала происходит выравнивание порядков: А = 0.1624500.103, В = 0.0017698.103, затем сложение мантисс: А+В = 0.1642198.103. В этой записи дробная часть мантиссы содержит не 5, а 7 значащих цифр, следовательно, последние две должны быть отброшены. Отбрасываемая часть суммы равна 0.98.10-2. Такое отбрасывание должно производиться, естественно, с округлением старшей части результата. Существуют и практически реализуются несколько правил округления. Простейший способ - отбрасывание младшей части результата А+В = 0.16421.103 = 164.21. Этот метод так и называется: отбрасывание младших разрядов. Более общепринятый способ - симметричное округление. Обозначим результат сложения так:
где p - порядок результата; q - количество значащих цифр в представлении числа. (В нашем случае F =0.16421.103, G =0.98.103-5=0.98.10-2, p =3, q =5) Тогда симметричное округление выполняется по правилу: результат
(В нашем случае gs =0.98≥0.5, поэтому Иногда применяется более точное правило округления, учитывающее Относительная ошибка округления, выполненного способом отбрасывания, выражается формулой Относительная ошибка симметричного округления: В старших поколениях ЭВМ, характеризуемых сравнительно низким быстродействием, применялся в основном алгоритм отбрасывания. В современных ЭВМ, особенно если они оснащаются сопроцессорами вещественной арифметики, применяется симметричное округление. Округление, учитывающее случай Следует учесть, что современные ЭВМ работают в двоичной системе счисления. Поэтому нормализованное представление чисел с плавающей точкой выглядит так:
Поэтому ошибка отбрасывания: Анализ ошибок и их распространения при выполнении «длинных» вычислений позволил сформулировать следующие рекомендации по снижению ошибок вычислений: 1. Если необходимо произвести сложение - вычитание длинной последовательности чисел, то надо работать сначала с наименьшими по модулю числами. 2. Если возможно, необходимо избегать вычитания почти равных чисел, т.к. это приводит к большим относительным ошибкам.
|

 . Например, число 5.673 в виде с плавающей точкой можно записать так:
. Например, число 5.673 в виде с плавающей точкой можно записать так: <1,
<1,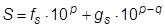 ,
, - старшая часть результата;
- старшая часть результата;  - младшая часть результата;
- младшая часть результата; с округлением равен
с округлением равен
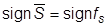 .
. .
. . Это, естественно, самая грубая ошибка из всех способов округления.
. Это, естественно, самая грубая ошибка из всех способов округления. , т.е. ошибка симметричного округления в среднем в два раза меньше ошибки отбрасывания.
, т.е. ошибка симметричного округления в среднем в два раза меньше ошибки отбрасывания. ,
, 
 ; ошибка симметричного округления:
; ошибка симметричного округления: