РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ
(по материалам ЕГЭ) Задача №1. Вычислите объём правильной треугольной пирамиды, если радиус описанной вокруг основания окружности равен
1) найдем сторону основания правильной пирамиды по формуле
2) найдем площадь основания, как площадь правильного треугольника
3) вычислим объём пирамиды
Ответ. 9
Задача №2. Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен Решение. 1) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. 2) найдем сторону основания правильной пирамиды по формуле 3) найдем площадь основания, как площадь правильного треугольника 4) из прямоугольного треугольника 5) вычислим объём пирамиды
Ответ. 18
Задача №3. Вычислите площадь боковой поверхности правильной треугольной пирамиды, если радиус описанной около основания окружности равен
1) найдем сторону основания правильной пирамиды по формуле 2) найдем периметр основания Р = 3· а, Р = 9. 3) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. 4) из прямоугольного треугольника МОР по теореме Пифагора находим апофему МР: МР = 5) вычислим площадь боковой поверхности правильной пирамиды:
Ответ.
Задача №4. Вычислите объём правильной треугольной пирамиды, сторона основания которой равна 6, а апофема пирамиды равна Решение. 1) найдем радиус описанной около основания и вписанной в основание окружностей: 2) найдем площадь основания, как площадь правильного треугольника 3) из прямоугольного треугольника МОР по теореме Пифагора находим высоту: 4) вычислим объём правильной пирамиды: Ответ. 18.
Решение. 1) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. 2) найдем сторону основания правильной пирамиды по формуле 3) найдем площадь основания, как площадь правильного треугольника 4) вычислим объём правильной пирамиды: Ответ. 36.
Задача №6. Вычислите площадь боковой поверхности правильной четырехугольной пирамиды, если её ребра равны 5, а радиус окружности, описанной вокруг основания равен 3
1) найдем сторону основания по формуле
2) найдем периметр основания: Р = 4 а, Р = 24.
3) из прямоугольного треугольника МDР по теореме Пифагора находим апофему МР: тогда: МР =
4) вычислим площадь боковой поверхности пирамиды: Ответ. 48.
Задача №7. В правильной четырехугольной пирамиде площадь боковой поверхности равна 16
Решение.
1) найдем сторону основания: так как в основании пирамиды квадрат с площадью равной 4, то сторона квадрата равна 2, а его периметр 8.
2) по условию
3) из прямоугольного треугольника МОР по теореме Пифагора находим высоту: Ответ.
Задача №8. Вычислите объём правильной шестиугольной пирамиды, если сторона основания равна 4, а боковые ребра пирамиды равны 5. Решение. 1) сторона основания правильного шестиугольника равна радиусу описанной около него окружности т.е.
2) площадь правильного шестиугольника найдем по формуле
3) из прямоугольного треугольника МОВ найдем высоту МО:
4) вычисляем объём пирамиды: Ответ. 24 Задача №9. В правильной шестиугольной пирамиде сторона основания равна 2
Решение.
1) найдем площадь правильного шестиугольника по формуле 2) из прямоугольного треугольника МОВ найдем высоту МО, учитывая, что в правильном шестиугольнике
3) вычисляем объём пирамиды:
Ответ: 24.
Задача № 10. Около правильной треугольной призмы описан цилиндр. Высота цилиндра равна 5, а радиус его основания R удовлетворяет уравнению R 2 + R – 6 = 0. Найдите объём призмы.
1) так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра, Н = 5. 2) по условию R удовлетворяет уравнению R 2 + R – 6 = 0, решая которое находим R 1 = - 3, R 2 = 2, так как радиус величина положительная то -3 не удовлетворяет условию задачи. 3) найдем сторону вписанного правильного треугольника по формуле 4) найдем площадь основания правильной призмы, как площадь правильного треугольника: Ответ. 15
Задача №11. Около правильной треугольной призмы описан цилиндр. Расстояние между осью цилиндра и стороной основания призмы равно
Решение. V = S · H 1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра, по условию Н = 3 R.. 2) Расстояние между осью цилиндра и стороной основания призмы равно радиусу вписанной в треугольник АВС окружности, т.е. 3) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. 4) найдем сторону вписанного правильного треугольника по формуле 5) найдем площадь основания правильной призмы, как площадь правильного треугольника: 6) вычислим объём призмы: V = S · H =S· 3 ·R = Ответ. 162. Задача №12. Около правильной треугольной призмы описан цилиндр. Площадь боковой поверхности цилиндра равна 16 p. Найдите объём призмы, если сторона её основания равна 5. Решение. V = S · H 1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра. 2) Найдем площадь основания правильной призмы, как площадь правильного треугольника: 3) Сторона вписанного правильного треугольника находится по формуле 4) По условию площадь боковой поверхности цилиндра равна 16·p т.е. 5) Вычислим объём призмы: V = S · H = Ответ. 30. Задача №13. Около правильной четырехугольной призмы описан цилиндр, площадь боковой поверхности которого равна 20p. Найдите площадь боковой поверхности призмы.
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра. 2) По условию площадь боковой поверхности цилиндра равна 20p, т.е. 3) так как призма правильная, то в её основании лежит квадрат, со стороной 4) вычислим площадь боковой поверхности призмы Ответ.
Задача №14. В правильную четырехугольную призму вписан цилиндр. Объем цилиндра равен 16
Решение. 1) Так как цилиндр вписан в призму, то высота призмы равна высоте цилиндра, а основание цилиндра вписано в основание призмы. 2) Так как радиус окружности, описанной вокруг основания призмы, равен а радиус цилиндра равен, радиусу вписанной в квадрат окружности и равен: 3) По условию объём цилиндра равен 16 4) Из прямоугольного треугольника АСА1 находим диагональ А1С: А1С = Ответ. 8.
1) Так как цилиндр вписан в призму, то высота призмы равна высоте цилиндра, а основание цилиндра вписано в основание призмы. 2) по условию радиус цилиндра 3) сторона правильного шестиугольника равна радиусу описанной около него окружности, т.е. 4) по условию площадь призмы равна 54 Pосн.·Н + 2 Sосн=54 5) найдем периметр основания и его площадь: Р = 6·а = 6 ·2 Sосн = 6) подставим полученные значения в формулу Pосн.·Н + 2 Sосн=54 Ответ. 1,5.
Задача № 16. Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 16 p, высота цилиндра равна 4. Найдите объём призмы.
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, т.е. Н = 4. 2) по условию
3) так как сторона правильного шестиугольника равна радиусу описанной около него окружности, то а = 2. 4) Найдем площадь основания призмы по формуле: 5) вычислим объём призмы: Ответ. 24 Задача №17. Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 10 p. Найдите объём цилиндра, вписанного в эту же призму.
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра.
2) по условию
3) так как сторона правильного шестиугольника равна радиусу описанной около него окружности, то R = а.
4) выразим радиус основания вписанного цилиндра 5) запишем формулу вычисления объёма вписанного в призму цилиндра: V = S · H, т.е.: V = Ответ. 7,5p. Задача №18. Около правильной четырехугольной призмы описан цилиндр. Объём цилиндра равен 24p. Найдите радиус цилиндра, если диагональ боковой грани призмы равна 5.
1) Так как призма правильная, то в её основании лежит квадрат, и радиус описанной окружности 2) по условию 3) из прямоугольного треугольника DCC 1 найдем СС 1 = Н по теореме Пифагора: Н = 4) приравняем значения для Н:
|

 , а высота пирамиды равна 4
, а высота пирамиды равна 4  Решение.
Решение.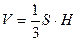 .
. ,
,  .
.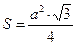 ,
, 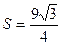 .
.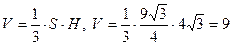 .
. , тогда
, тогда  .
. .
. .
. по теореме Пифагора находим высоту пирамиды:
по теореме Пифагора находим высоту пирамиды:  ,
,  .
. .
. .
. Решение.
Решение.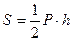
 .
. ,
,
 .
. .
. .
.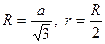 то есть
то есть  .
. .
. , МО =
, МО =  .
.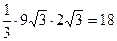 .
. .
. .
. .
. .
. .
. Решение.
Решение.  , т.е.
, т.е.  .
. , DP =
, DP = 
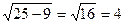 .
. .
.
 = 16
= 16  .
. = 1, получаем: МО =
= 1, получаем: МО =  .
. .
.
 ,
, 
 или
или  = 24
= 24  .
. .
. . Найдите объём пирамиды.
. Найдите объём пирамиды.
 .
. .
. Решение. V = S · H
Решение. V = S · H ,
,  .
. =
= 
 .
.
 , и по условию равно
, и по условию равно 
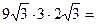 162.
162. .
.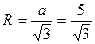 .
. , откуда Н =
, откуда Н =  =
=  .
. Решение.
Решение. 
 ,
,  .
.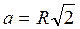 , тогда периметр основания равен
, тогда периметр основания равен  .
.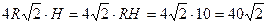 .
. .
.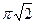 , а радиус окружности, описанной вокруг основания призмы, равен
, а радиус окружности, описанной вокруг основания призмы, равен  . Найдите диагональ призмы.
. Найдите диагональ призмы.
 =
= 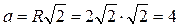

 ,
,  = 4
= 4  .
. Задача №15. В правильную шестиугольную призму вписан цилиндр. Найдите высоту призмы, если её площадь равна 54
Задача №15. В правильную шестиугольную призму вписан цилиндр. Найдите высоту призмы, если её площадь равна 54  равен 3, тогда
равен 3, тогда  ,
,  .
. .
. .
. Решение. V = S · H
Решение. V = S · H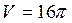 , т.е.
, т.е. , R = 2.
, R = 2. =6
=6  .
.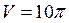 , т.е.
, т.е. .
. через радиус описанного цилиндра
через радиус описанного цилиндра 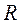 :
: 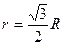 .
. =p·
=p·  .
. Решение.
Решение. равен половине диагонали АС, или
равен половине диагонали АС, или  , где а – сторона квадрата.
, где а – сторона квадрата. , т.е.
, т.е.  = 24p, или
= 24p, или  , или
, или 
 .
. ,
,


