Тепловые балансы теплообменных аппаратов
Тепловую нагрузку теплообменного аппарата или количество теплоты, переданной от горячего теплоносителя к холодному в единицу времени, можно определить по уравнению теплового баланса. В общем виде уравнение теплового баланса имеет вид - для идеального теплового процесса (без учета потерь теплоты в окружающую среду) Q = Q1 = Q2; (1) - для реального теплового процесса (с учетом потерь теплоты в окружающую среду) Q1 = Q2 + Qпот. (2) Здесь Q1 – количество теплоты, отданной горячим теплоносителем, Вт; Q2 – количество теплоты, сообщенной холодному теплоносителю, Вт; Qпот – потери теплоты в окружающую среду, Вт. При наличии теплоизоляции тепловые потери незначительны, поэтому в расчете их можно не учитывать. Для теплообмена, протекающего без изменения фазового состояния теплоносителей, уравнение теплового баланса имеет вид G1C1(t1н – t1к) = G2C2(t2к – t2н), (3) где G1; G2 – массовый расход горячего и холодного теплоносителей соответственно, кг/с; t1н; t1к – температура горячего теплоносителя на входе (начальная температура t1н) и на выходе (конечная температура t1к), град; t2н; t2к – то же самое для холодного теплоносителя; С1 – удельная теплоемкость горячего теплоносителя при средней температуре tср1, кДж/(кг. град); С2 – то же самое для холодного теплоносителя при tср2. Из уравнения (3) определяется неизвестный расход одного из теплоносителей или неизвестная температура одного из теплоносителей. Например - расход холодного теплоносителя определится по выражению
- температура горячего теплоносителя на выходе из аппарата
При изменении фазового состояния одного из теплоносителей (например, конденсация насыщенного водяного пара) уравнение теплового баланса запишется в виде
где r1 – удельная теплота конденсации, кДж/кг. (свойства насыщенного водяного пара приведены в таблице I приложения); х1 – степень сухости пара. При конденсации перегретого пара с охлаждением конденсата тепловая нагрузка будет равна Q = Qпер + Qконд + Qохл. (7) Здесь Qпер = G1Cп(t1н – tнас) – количество теплоты, отдаваемой при охлаждении перегретого пара; Qконд = G1r – количество теплоты, отдаваемой при конденсации пара; Qохл = G1Cж(tнас – t1к) – количество теплоты, отдаваемой при охлаждении конденсата; tнас – температура насыщенного пара; Сп – теплоемкость пара; Сж – теплоемкость конденсата. Средняя температура теплоносителя, фазовое состояние которого не меняется, можно определить как среднеарифметическую между начальной и конечной температурами tср i = Более точное значение средней температуры одного из теплоносителей определяется из уравнения tср i = tj ± Dtср, (9) где tj – среднеарифметическая температура теплоносителя с меньшим перепадом температуры вдоль поверхности теплообмена; Dtср – средняя разность температур теплоносителей, град. Уравнение (1.9) справедливо и при изменении фазового состояния теплоносителя (кипение или конденсация), когда его температура вдоль поверхности теплопередачи остается постоянной и зависит от давления и состава теплоносителя.
|

 ; (4)
; (4) . (5)
. (5)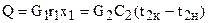 , (6)
, (6)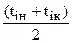 , i = 1, 2. (8)
, i = 1, 2. (8)


