ИЗБЫТОЧНОСТЬ ПРЕДСТАВЛЕНИЙ БЕРНУЛЛИЕВСКИХ ИСТОЧНИКОВ
И.А. Косенков (студент гр. САПР-51) Научный руководитель: д.ф-м.н.,профессор, КФ МГТУ им.Н.Э.Баумана А.К. Горбунов Решение многих задач быстрого анализа цифровых массивов данных связано с получением их представлений в виде совокупностей фрагментов и кодированием таких представлений (1). Примерами такой обработки являются процедуры сжатия последовательностей отсчетов на основе отбора их существенных значений, процедуры разбиения изображений или многомерных спектров измерений на однородные фрагменты, которые образуют смысловые единицы последующего анализа. Очевидно, что быстродействие анализа тем вше, чем меньше фрагментов в представлении массива. Поэтому возникает задача оптимизации фрагментного представления, цель которой найти в задаyном классе способов разбиения такой, который обеспечивал бы наименьшее количество фрагментов в каждом массиве. Целесообразно исследовать также представления, которые могут быть не оптимальны в указанном смысле, но обладают свойством иерархической упорядоченности фрагментов. Такие структуры удобны для организации размена быстродействия анализа на точность. В настоящей работе исследуется среднее количество фрагментов, получаемых на оптимальном и близком к нему древовидном (2) представлениях многомерных бернуллиевских массивов. Приводятся оценки энтропии таких представлений, определяющей минимальные средние затраты (в битах) на их кодирование. Формализация задачи. Пусть Введем среднюю сложность представления (на элемент массива) при способе разбиения
и минимальную среднюю сложность
которая достигается при оптимальном разбиение
где суммирование производиться по множеству всех фрагментов, получаемых на разбиении Оценка сложности и энтропии. Для указанных представлений (1)-(3), при
при
для минимального представления
При n>1 верхние оценки сложностей
то имеет место оценка
Суммирование в (6) и (7) производится по всем значениям
Вычисление энтропии (3) для распределения (6) с учетом соотношений (7) и (8) при
где
и При n=1 и Таким образом, фрагментное представление с большей избыточностью сложности имеет меньшую избыточность энтропии. Так при n=1 и
|

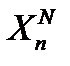 - множество порождаемых источником n- мерных массивов, которые по каждой координате содержат N элементов двоичного алфавита {0,1}. Пусть
- множество порождаемых источником n- мерных массивов, которые по каждой координате содержат N элементов двоичного алфавита {0,1}. Пусть 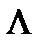 - множество способов разбиения массивов на однородные фрагменты так, что при любом
- множество способов разбиения массивов на однородные фрагменты так, что при любом  массив
массив 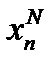 представлен совокупностью фрагментов
представлен совокупностью фрагментов 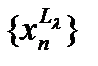 , каждый из которых состоит из одинаковых элементов.
, каждый из которых состоит из одинаковых элементов.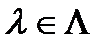
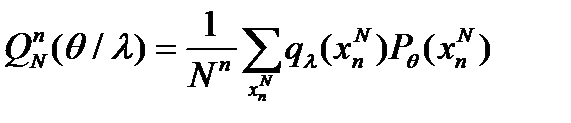 (1)
(1)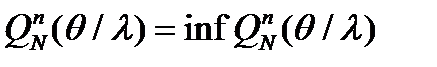 (2)
(2)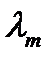 . Минимальные затраты на кодирование фрагментного представления определяются отношением энтропии ансамбля его фрагментов к среднему количеству элементов фрагмента. Эта величина равна
. Минимальные затраты на кодирование фрагментного представления определяются отношением энтропии ансамбля его фрагментов к среднему количеству элементов фрагмента. Эта величина равна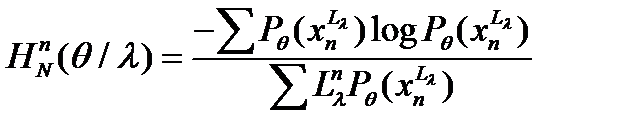 (3)
(3)
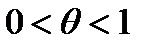 . В случае n=1 получены точные значения этих функций, в случае n>1- верхние и нижние оценки энтропии. Для средних сложностей минимального и древовидного представлений последовательностей найдены рекуррентные соотношения:
. В случае n=1 получены точные значения этих функций, в случае n>1- верхние и нижние оценки энтропии. Для средних сложностей минимального и древовидного представлений последовательностей найдены рекуррентные соотношения: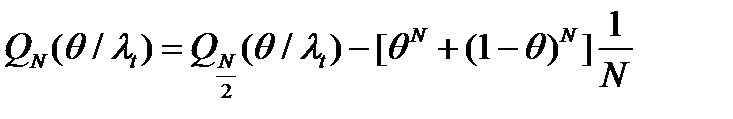
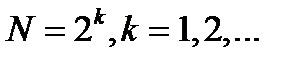 .Учитывая, что в обоих случаях
.Учитывая, что в обоих случаях 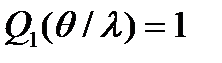 , из рекуррент имеем
, из рекуррент имеем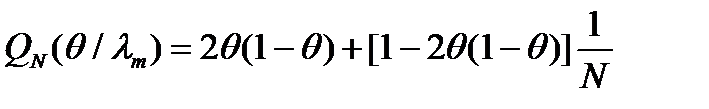 (4)
(4)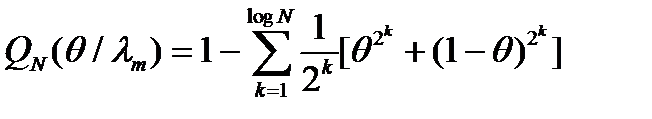 (5)
(5)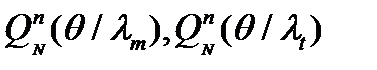 равным n-ым степеням правых частей (4) и (5).
равным n-ым степеням правых частей (4) и (5).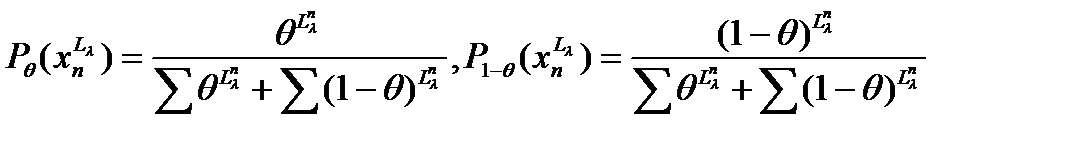 (6)
(6)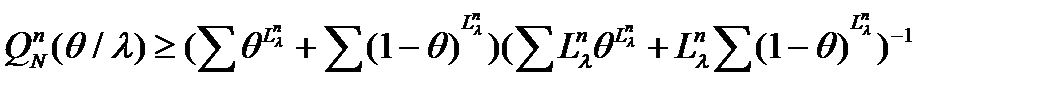 (7)
(7)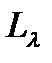 , получаемым на разбиении
, получаемым на разбиении 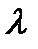 .
.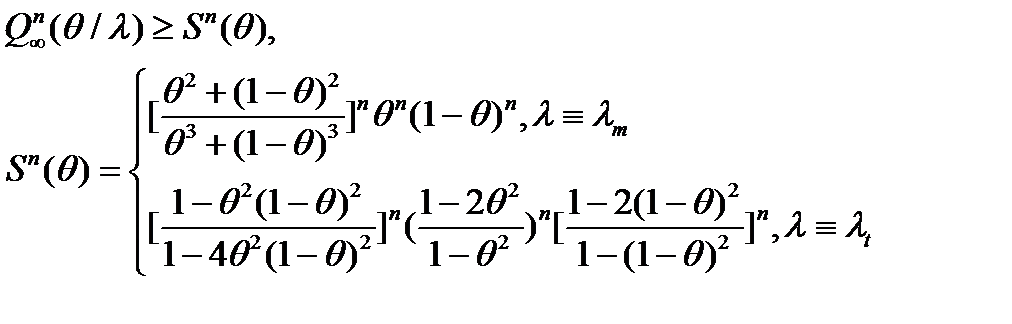 (8)
(8)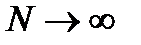 приводят к оценкам следующего вида
приводят к оценкам следующего вида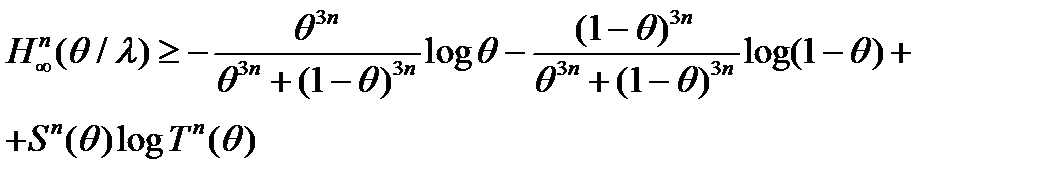 (9)
(9)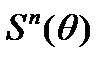 определенно в (8), а
определенно в (8), а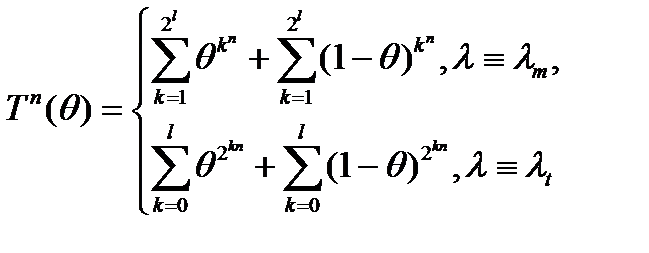
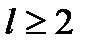 . Увеличение l приводит к уточнению оценок (9).
. Увеличение l приводит к уточнению оценок (9).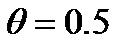 (9) выполняется со знаком равенства для минимального преставления и дает
(9) выполняется со знаком равенства для минимального преставления и дает 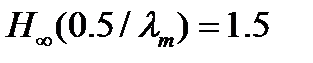 бита.
бита.


