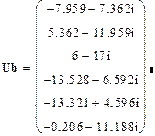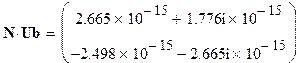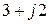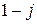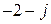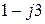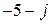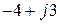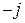Пример выполнения
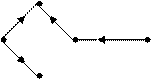
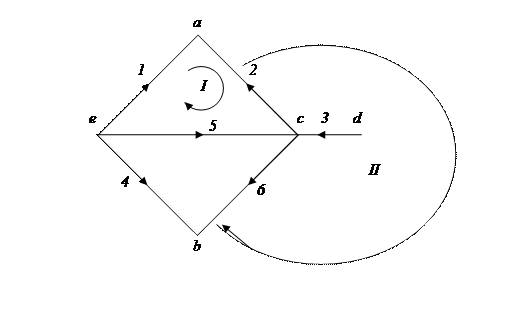
ВАРИАНТ ЗАДАНИЯ Базисный узел Заданный Базисный узел Заданное множество хорд 2. Формируется множество хорд и Строится остов дерева. (остов дерева берется согласно варианта Задания. В рассматриваемом примере
3. Назначается балансирующий узел; (Балансирующий узел назначается согласно № варианта Задания. В рассматриваемом примере балансирующий узел 4. Вводится новая нумерация ребер направленного графа так, чтобы сперва нумеровались ветви остова, а затем хорды; 5. Вводится новая нумерация вершин направленного графа так, чтобы балансирующий узел стал последним;
6. Для заданного варианта комплексных сопротивлений ветвей
и для новой нумерации ветвей Формируется диагональная матрица;
На диагонали должны стоять комплексные сопротивления соответствующие новой нумерации. 7. Для заданного варианта комплексных задающих токов в узлах,
и новой нумерации узлов формируется вектор задающих токов
В рассматриваемом примере токи не заново не перенумеровываются, так как базисный последний. 8. Строится расширенная матрица инцидентности В рассматриваемом примере
Строится блочная усеченная матрица инцидентности Матрица Блочная Матрица инцидентности для рассматриваемого примера
9. Находится обратная матрица транспонированной блока
10. Находится блок матрицы контуров
11. По заданным хордам строятся независимые контура, так чтобы направления обхода совпадало с направлением соответствующей хорды, а порядок нумерации независимых контуров - с порядком нумерации ветвей (хорд). 12. Строится блочная матрица контуров Если хорды и независимые контура сонаправлены, то по предыдущему пункту 11
поэтому искомая матрица
Правильность построения матрицы Первый контур Второй контур
Кроме того, должно выполняться условие ортогональности
13. Вычисляются коэффициенты матрицы контурных сопротивлений, и формируется соответствующая матрица контурных сопротивлений
Проверить полученный результат, используя свойства матрицы контурных сопротивлений
14. Вычисляется матрица сопротивлений (размера
и вектор эквивалентных ЭДС
для задающих токов. 15. Формируется система контурных уравнений
при отсутствии ЭДС в ветвях (
16. Решается система контурных уравнений, и находятся контурные токи
17. Найдя контурные токи и, зная токи в независимых узлах, найдем токи в ветвях остова (токи в хордах равны токам в независимых контурах)
18. Формируется вектор токов в ветвях
19. Для проверки правильности решения определим задающие токи
20. По закону Ома вычисляем вектор напряжения ветвей
. 21. проверим 2 закон Кирхгофа
Варианты
Номер варианта по номеру списка в журнале.
Сопротивления ветвей
Задающие токи
|

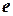 множество хорд
множество хорд 
 )
)


 )
)

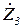


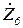
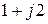

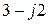
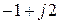
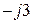

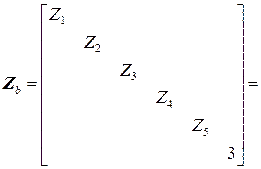
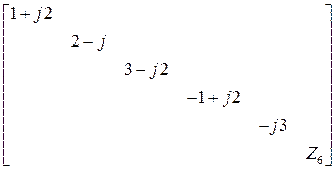

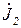
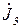

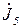
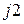


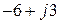
 ;
;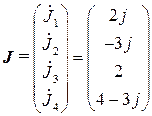
 ;
;
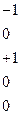
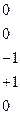

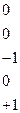
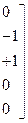


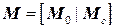 ;
; ) и перестановки столбцов так, чтобы последние столбцы соответствовали хордам варианта (в данном примере хорды 5 и 6, и столбцы не переставляются).
) и перестановки столбцов так, чтобы последние столбцы соответствовали хордам варианта (в данном примере хорды 5 и 6, и столбцы не переставляются).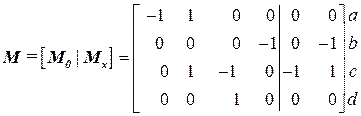
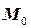 матрицы инцидентности, который соответствует остову;
матрицы инцидентности, который соответствует остову;
 , который соответствует остову;
, который соответствует остову;
 ;
;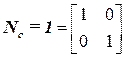
 ,
, примет вид
примет вид
 .
. 







 ;
;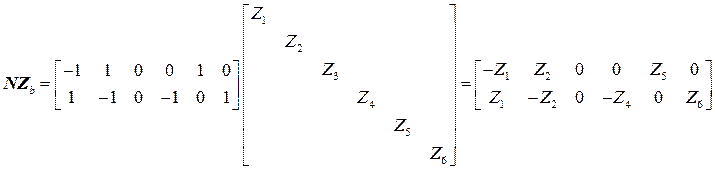
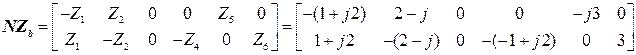
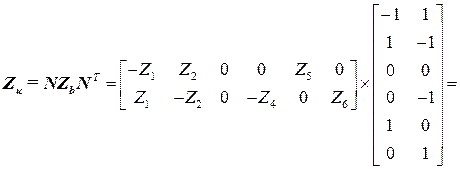
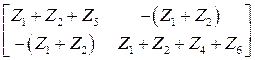
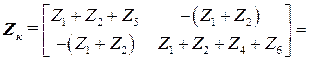


 ) для вектора
) для вектора 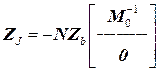 =
= 
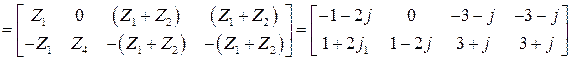
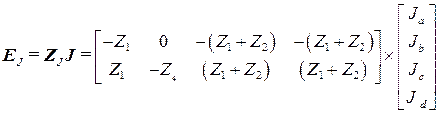
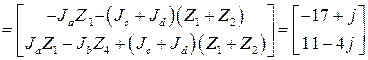
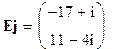

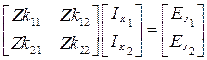
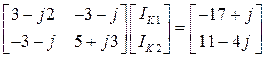
 )
) .
.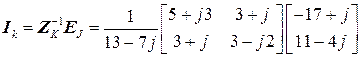
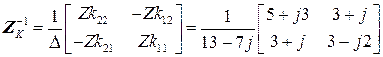

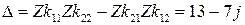

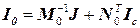
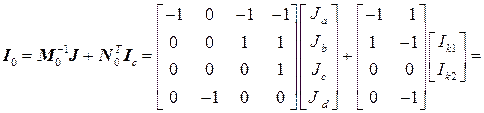
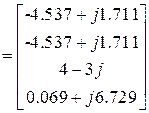
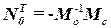
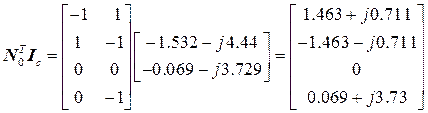



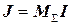 (проверим 1 закон Кирхгофа
(проверим 1 закон Кирхгофа 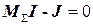 )
)
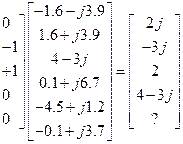
 ;
;