Числовые модели

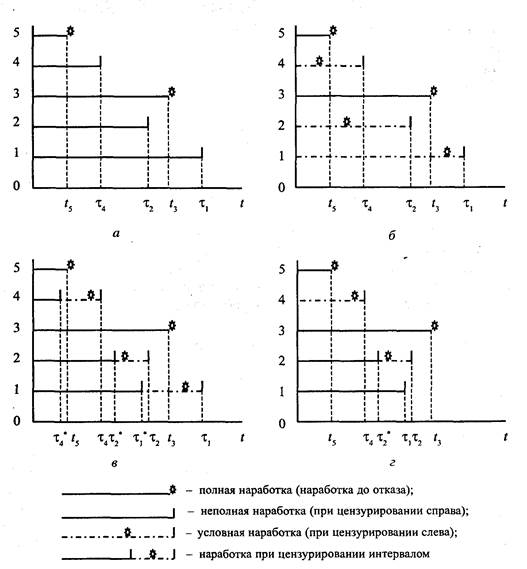
Числовые модели отличаются от классификационных рядом особенностей:

1) целевые признаки х₀ измеряются в числовых шкалах;

2) числа x_Q представляют собой функционалы или функции признаков переменных, которые не обязательно имеют числовые выражения;

3) в числовых моделях переменные могут зависеть от времени.

Если в задаче классификации для получения экспериментальной информации необходимо организовывать наблюдения за группой однотипных объектов, то в задаче построения числовых моделей в качестве первичной информации могут присутствовать результаты длительных наблюдений за одним объектом или небольшой по объему группой однотипных объектов. Числовые модели могут задавать связь между переменными как в виде параметрических, так и в виде непараметрических зависимостей. Типичными задачами для числовых моделей являются задачи косвенных измерений и поиска экстремума.

В задаче косвенных измерений (или как ее еще называют задачей оценки параметров) требуется по результатам наблюдений {д: } оценить параметр х₀. В отличие от задачи классификации х₀ измеряется не в номинальной шкале, а в числовой. Если статистические данные ЦД представляют собой результаты наблюдения до некоторого момента времени t₀, ах₀ требуется оценить для момента t > t₀, то задача оценивания называется прогнозированием.

Задача поиска экстремума состоит в организации наблюдений за исследуемым процессом таким образом, чтобы по результатам наблюдений {х.р_к)}, t_k = t_o+kAt, к = 0, 1, 2,... можно было получить экстремальное значение целевого признака д:₀. Задачи такого рода решаются с помощью методов планирования эксперимента.

6.4. Вероятностное описание событий и процессов

Экспериментальные исследования проводят с целью получения новых сведений об объекте анализа. Экспериментальные данные необходимы для того, чтобы устранить неопределенность в знаниях об объекте, для которого производится построение модели. Основной причиной неопределенности является случайность явлений и процессов, происходящих в объектах исследования. Совершенно очевидно, что в природе нет ни одного физического явления, в котором не присутствовали бы в той или иной степени элементы случайности. Как бы точно и тщательно ни были бы фиксированы условия проведения эксперимен-

та, невозможно достигнуть того, чтобы при повторении опыта результаты полностью и в точности совпадали. Случайные отклонения неизбежно сопутствуют любому закономерному явлению. В ряде практических задач этими случайными элементами можно пренебречь, предполагая, что в данных условиях проведения наблюдений явление протекает вполне определенным образом. При этом из множества воздействующих на процесс факторов выделяются самые главные, влиянием остальных факторов пренебрегают. В других исследованиях исход опыта зависит от большого количества факторов, к тому же на исход эксперимента влияют не только сами факторы, но и их сочетание, их взаимодействие. В результате приходим к необходимости изучения случайных явлений, исследованию закономерностей и выяснению причин возникновения случайностей в наблюдаемом явлении. При рассмотрении результатов отдельных экспериментов бывает трудно обнаружить какие-либо устойчивые закономерности. Однако, если рассмотреть последовательность большого числа однородных экспериментов, можно обнаружить некоторые интересные свойства, а именно: если индивидуальные результаты опытов ведут себя непредсказуемо, то средние результаты обнаруживают устойчивость.

Случайность можно определить как вид неопределенности, подчиняющейся некоторой закономерности, которая выражается распределением вероятностей. Зная распределение вероятностей, можно ответить на следующие вопросы: в каком интервале находятся возможные значения случайной величины, каково наиболее вероятное значение случайной величины, каково рассеивание реализовавшихся случайных величин, какова связь между разными реализациями и т.д. Но для того, чтобы определить закон или плотность распределения случайной величины, необходима информация об исследуемом объекте. В основе проведения любых расчетов лежат исходные данные, результаты наблюдений случайной величины или случайного процесса. Измерения случайных величин и процессов по существу есть измерение выходного параметра, характеризующего определенные свойства объекта исследования. На основании таких измерений решаются вопросы восстановления вида и параметров законов распределения, вычисление коэффициентов регрессии и корреляции, восстановление спектральных плотностей и тому подобные расчеты.

Следует отметить, что результаты наблюдений за функционированием сложных систем, каковые являются, в первую очередь, объектом системного анализа, имеют ряд специфических особенностей, приводящих к необходимости применения и разработки неклассических методов анализа. Остановимся на рассмотрении данных особенностей.

Большая размерность массива данных. Для построения модели сложной системы требуется проводить наблюдения за большой группой выходных параметров, причем некоторые параметры могут характеризоваться рядом признаков. Существенным является также необходимость учета фактора времени, т.е. фиксация изменения свойств объекта в зависимости от времени жизни системы. Современные методы организации баз данных на ЭВМ способны решать задачи сбора и хранения данных, но тем не менее проблема размерности все-таки остается.

Разнотипность данных. Разные признаки могут измеряться в различных шкалах. Здесь возникает проблема согласования данных.

Зашумленность данных. Наблюдаемая величина отличается от истинного значения параметра на некоторую случайную величину. Примерами таких зашумляющих факторов могут служить дрейф нуля измерительного прибора, погрешности приборов, наличие помех в каналах передачи информации и т.п. Статистические свойства помех могут не зависеть от измеряемой величины, тогда помехи можно рассматривать как аддитивный шум. В противном случае имеет место неаддитивная или зависимая помеха. Различные варианты зашумленности должны по-разному учитываться при разработке алгоритмов обработки данных.

Отклонения от предположений, искажения результатов. Приступая к обработке данных, аналитик всегда исходит из определенных предположений о природе величин, подлежащих обработке. Любой способ обработки дает результаты надлежащего качества только в том случае, когда обрабатываемые данные отвечают заложенным в алгоритм обработки предположениям. Во-первых, большинство наблюдаемых параметров имеет характер непрерывных величин, но при обработке неизбежно округление данных, что может привести к искажениям результатов. Далее - измерительный прибор может обладать нелинейной характеристикой и если это не учитывается в алгоритме обработки, то итоговые данные будут также иметь искажения. Чтобы повысить качество выводов, получаемых при обработке данных, необходимо обеспечить соответствие свойств данных и требований к алгоритмам их обработки.

Наличие пропущенных значений. Данная ситуация имеет место в том случае, когда часть наблюдений не доводится до реализации наблюдаемого признака. Примерами таких ситуаций могут служить эксперименты по определению надежности группы однотипных изделий. Современные изделия обладают достаточно высоким уровнем надежности и даже длительные по времени наблюдения за их функционированием не приводят к отказам всей совокупности изделий. В результате выборка данных будет иметь характер цензурированной выборки, в которой для части изделий имеется информация о времени их отказа,

для другой же части такой информации нет. Другим примером могут служить социологические исследования, которые допускают либо отсутствие определенных сведений об опрашиваемых субъектах, предполагают возможность неконкретного ответа на вопросы (типа «не знаю»).

Отмеченные особенности поступающей для обработки статистической информации накладывают определенные ограничения на выбор методов и предъявляют требования к разработке специальных алгоритмов ее обработки.

Одним из подходов, позволяющих учитывать различного рода неопределенности при обработке статистической информации, явилась теория статистического интервального оценивания. Ключевым при построении вероятностных моделей является утверждение о том, что в строгом смысле точные средние и вероятности - это параметры статистически устойчивого явления и достигаются они усреднением при неограниченном повторении того же самого явления в независимых и устойчивых условиях. Так как организовать устойчивое повторение затруднительно, а неограниченное число раз просто невозможно, то часто подразумевают мыслимый повтор. Но чтобы проиграть явление в уме или на ЭВМ, нужно более или менее знать физическую модель явления. Реальные же явления таковы, что их внутренние механизмы до конца не поддаются исследованиям, опыты уникальны, их повторы неустойчивы. В результате точные характеристики остаются как идеальное понятие, достигаемое в пределе, применение которого сопровождается многими оговорками. Таким образом, не только неустойчивость явлений, но и любая неабсолютность статистических знаний, такая как недостаточность, неточность, ограниченность, свойственная почти всем реальным задачам, естественно вынуждает переходить к интервальным понятиям.

В отличие от теории вероятностей, освещающей поточечную структуру моделей, интервальный анализ оперирует только имеющейся информацией, всегда конечной, представленной в интервальной, размытой, доверительной форме.

6.5. Описание ситуаций с помощью нечетких моделей

Одна из основных целей построения математических моделей реальных систем состоит в поиске способа обработки имеющейся информации либо для выбора рационального варианта управления системой, либо для прогнозирования путей ее развития. При решении задач системных исследований достаточно часто, особенно при исследовании экономических, социальных, социотехнических систем, в функционировании которых принимает участие человек, значительное количество информации о системе получают от экспертов, имеющих опыт работы с данной или подобными системами, знающих ее особенности и имеющих представление о целях ее функционирования. Эта информация носит субъективный характер и ее представление в терминах естественного языка содержит большое число неопределенностей - «много», «мало», «высокий», «низкий», «очень эффективный» и т.п., которые не имеют аналогов в терминах языка классической математики. Язык традиционной математики, опирающийся на теорию множеств и двузначную логику, недостаточно гибок для представления встречающихся неопределенностей в характеристике объектов. В нем нет средств достаточно адекватного описания понятий, которые имеют неопределенный смысл. Представление подобной информации на языке традиционной математики обедняет математическую модель исследуемой реальной системы и делает ее слишком грубой. В классической математике множество понимается как совокупность элементов (объектов), обладающих некоторым общим свойством, например, множество чисел, не меньших заданного числа, множество векторов, сумма компонент каждого из которых не превосходит единицы и т.д. Для любого элемента при этом рассматривается лишь две возможности: либо элемент принадлежит множеству, т.е. обладает данным свойством, либо не принадлежит множеству и соответственно не обладает рассматриваемым свойством. Таким образом, в описании множества в обычном смысле должен содержаться четкий критерий, позволяющий судить о принадлежности или непринадлежности любого элемента данному множеству. Разработка математических методов отражения нечеткости исходной информации позволяет построить модель, более адекватную реальности. Одним из начальных шагов на пути создания моделей, учитывающих нечеткую информацию, считается направление, связанное с именем математика Л. Заде [34] и получившее название теории нечетких множеств. Лежащее в основе этой теории понятие нечеткого множества предлагается в качестве средства математического моделирования неопределенных понятий, которыми оперирует человек при описании своих представлений о реальной системе, своих желаний, целей и т.д. Нечеткое множество - это математическая модель класса с нечеткими или размытыми границами. В этом понятии учитывается возможность постепенного перехода от принадлежности к непринадлежности элемента рассматриваемому множеству. Иными словами, элемент может иметь степень принадлежности множеству, промежуточную между полной принадлежностью и полной непринадлежностью. Понятие нечеткого

множества - это попытка математической формализации нечеткой информации с целью ее использования при построении математических моделей сложных систем. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, обладающие общим свойством, могут обладать этим свойством по-разному, в большей или меньшей степени. При таком подходе высказывания типа «элемент принадлежит данному множеству» теряют смысл, поскольку необходимо указать «насколько сильно» или с какой степенью данный элемент принадлежит рассматриваемому множеству. Одним из важных направлений применения этого нового подхода является проблема принятия решений при нечеткой исходной информации.

Идеи теории нечетких множеств нашли развитие в теоретическом направлении, называемом статистикой объектов нечисловой природы. Особенностью этих объектов является то, что для них не определена совокупность арифметических операций. Объекты нечисловой природы лежат в пространствах, не имеющих векторной структуры.

Примерами объектов нечисловой природы являются:

• значения качественных признаков, т.е. результаты кодировки объектов с помощью заданного перечня категорий (градаций);

• упорядочения (ранжировки) экспертами образцов продукции (при оценке ее технического уровня);

• классификации, т.е. разбиения объектов на группы сходных между собой (кластеры);

• бинарные отношения, описывающие сходство объектов между собой, например, сходство тематики научных работ, оцениваемое экспертами с целью рационального формирования экспертных советов внутри определенной области науки;

• результаты парных сравнений или контроля качества продукции по альтернативному признаку («годен» - «брак»), т.е. последовательности из нулей и единиц;

• множества (обычные или нечеткие), например, зоны, пораженные коррозией, или перечни возможных причин аварии, составленные экспертами независимо друг от друга;

• слова, предложения, тексты;

• векторы, координаты которых представляют собой совокупность значений разнотипных признаков, например, результат составления статистического отчета о научно-технической деятельности или заполненная компьютеризированная история болезни, в которой часть признаков носит качественный характер, а часть - количественный;

• ответы на вопросы экспертной, маркетинговой или социологической анкеты, часть из которых носит количественный характер (возможно, интервальный), часть сводится к выбору одной из нескольких подсказок, а часть представляет собой тексты и т.д.

Статистические методы анализа нечисловых данных нашли широкое применение в экономике, социологии, при проведении экспертного анализа. Дело в том, что в этих областях от 50 до 90% данных являются нечисловыми.

6.6. Характеристика и классификация статистической информации

Классическая схема обработки результатов наблюдений, состоит в предположении, что в каждом испытании реализуется наблюдаемый признак. Например, при испытании объектов на надежность каждый объект доводится до отказа. Такая схема является идеализацией реально проводимых исследований. В реальной жизни, в особенности при проведении обследования функционирующих объектов, информация, поступающая на обработку, крайне ограничена. Например, при эксплуатации объектов их стараются не доводить до отказа. Более того, на предприятии, как правило, существует система предупредительных профилактических мероприятий, суть которых заключается в том, чтобы не допустить возникновение отказов изделий в процессе их функционирования. Даже при организации специальных экспериментов с целью определения характеристик надежности партии испытываемой продукции не удается всю партию довести до отказа, так как для этого потребовалось бы большое время проведения эксперимента. Аналогичные данные поступают на обработку и в других областях проведения исследований. Например, в области социологии или психологии для части испытуемых рассматриваемый признак может наблюдаться, для части - нет (скажем, при определении среднего возраста вступления в брак часть анкетируемых может ответить, что до настоящего времени в браке не состоит). При проведении исследований в медицине у части больных за время наблюдения исследуемый признак может не реализоваться. Так, если анализируется воздействие некоторого препарата на состояние больного и фиксируется время, в течение которого наступает выздоровление, то у одних пациентов процесс выздоровления может пойти быстро, у других медленнее, а у некоторой части за время наблюдения он может не наступить. Возможно он реализуется в дальнейшем, но вывод о результатах исследования формируется в данный момент времени и часть наблюдений, таким образом, является не доведенной до конца. Но, несмотря на то, что для части объектов исследования яв-

ляются не доведены до конца, в них содержится полезная информация, которую необходимо использовать при обработке результатов наблюдений. Данные, для которых имеется неопределенность в наблюдениях за реализацией исследуемого признака, называются цензурирован-ными данными.

Цензурирование - это процесс возникновения неопределенности момента реализации признака объекта (в теории надежности момента отказа), причем интервал неопределенности считается известным. Интервалом неопределенности называется интервал времени, внутри которого произошла либо произойдет реализация наблюдаемого признака объекта, при этом точное значение времени реализации признака объекта неизвестно.

Понятие о цензурированной выборке

Рассмотрим основные понятия и определения, применительно к информации, поступающей на обработку на примере задачи оценивания показателей надежности.

" В процессе анализа надежности приходится сталкиваться с ситуациями, когда определенная часть объектов или систем не отказывает за период наблюдения, а другая часть отказывает, но моменты отказов точно неизвестны. В таких ситуациях возникает необходимость проведения статистического анализа надежности на основе специфических выборок, основной особенностью которых является отсутствие сведений о моментах отказов контролируемой части изделий. Это явление носит название цензурированных данных, а получаемые в результате выборки - цензурированными выборками (ЦВ).

Под данными, применительно к задачам надежности, понимают фиксированные значения наработок изделий, полученные по результатам испытаний или эксплуатационных наблюдений. Данными цензурированной выборки являются наработки как отказавших объектов, так и неотказавших объектов, а также интервалы времени, в течение которых объект отказал, но момент отказа точно неизвестен.

Цензурированной выборкой называется выборка, элементами которой являются значения наработки до отказа и наработки до цензурирования, либо только значения наработки до цензурирования. Как было отмечено ранее, цензурирование - это процесс возникновения неопределенности момента отказа объекта, причем интервал неопределенности известен аналитику. Интервал неопределенности - интервал наработки, внутри которого произошел либо произойдет отказ объекта, причем точное значение наработки до отказа неизвестно. Этот интервал может быть неограниченным справа, тогда говорят о цензурировании справа, либо ограниченным справа, тогда говорят о цензурировании слева. Если интервал неопределенности момента отказа ограничен слева и справа, то говорят о цензурировании интервалом. Следует отметить, что в задачах надежности при цензурировании слева левая граница интервала неопределенности равна нулю, а при цензурировании интервалом - больше нуля. На рис. 6.1 приведены реализации случайных наработок изделий до отказа и до цензурирования.

 

Рис. 6.1. Распределение значений наработок объектов для цензурированной

выборки:

а - справа; б - слева; в - интервалом; г – комбинированного

Необходимо обратить внимание на то, что цензурирование интервалом является наиболее общим видом цензурирования, так как при устремлении правой границы интервала к бесконечности этот вид цензурирования превращается в цензурирование справа, а при устремлении левой границы интервала к нулю - в цензурирование слева. При устремлении границ интервала друг к другу цензурирование исчезает.

Рассмотрим понятие «наработка». Полная наработка - это наработка изделия до отказа. Неполная наработка - наработка объекта от начала испытаний или эксплуатации до прекращения испытаний или эксплуатационных наблюдений до отказа. Условная наработка при цензурировании слева - это значение интервала, измеряемого в единицах наработки, в пределах которого произошел отказ. Эта наработка названа условной потому, что объект может не работать в пределах всего интервала, так как отказ может наступить в некоторой части этого интервала. Наработка при цензурировании интервалом складывается из неполной наработки и условной наработки при цензурировании слева.

Причины появления цензурированных данных

Отметим причины появления цензурированных данных на примере обработки результатов наблюдений с целью определения характеристик надежности объектов. Причиной появления цензурированных данных в данном случае является специфика организации функционирования объектов, состоящая в том, что реально функционирующие объекты в процессе работы до отказа стараются не доводить. На предприятии регулярно проводятся планово-профилактические работы (ППР), цель которых состоит в восстановлении работоспособности объектов. В большинстве случаев схема функционирования элементов следующая: в период проведения ППР объекты выводят из работы и на их место ставят новые. Работоспособность снятых объектов восстанавливается до первоначального уровня; если есть необходимость, производят их ремонт, настройку, чистку и прочие мероприятия. При проведении следующих ППР эти устройства ставятся в систему, а объекты, которые находились в работе, выводят для проведения восстановительных мероприятий. Особенностью функционирования является также наличие контроля исправности работы элементов, их замена при достижении определенной наработки, независимо от того, отказал элемент к данному моменту или нет.

Рассмотрим более детально причины возникновения цензурированных данных.

1. Разное время установки в систему и снятие с эксплуатации однотипных объектов. Такая схема организации эксплуатации характерна для элементов, которые выводятся из работы в период проведения ППР независимо от того, отказали они или нет; на их место устанавливаются аналогичные объекты из состава запасных изделий. Указанный режим организации эксплуатации имеет место для большинства объектов системы управления и защиты (СУЗ) энергоблоков АЭС, для ряда контрольно-измерительных приборов и устройств автоматики. Другой причиной может служить наличие резервных каналов и технологических петель, которые временно выводятся из работы и включаются в случае обнаружения отказа на работающем оборудовании.

2. Снятие объектов с эксплуатации из-за отказов составных частей, надежность которых не исследуется. Например, при оценке надежности различных устройств СУЗ, таких как устройство задания мощности, устройство измерения и контроля и т.п., они могут быть сняты с эксплуатации из-за отказов блоков питания, находящихся в соответствующих схемах каналов СУЗ.

3. Переход объектов из одного режима применения в другой в процессе их эксплуатации. Часть объектов используется в течение определенного промежутка времени, и далее наблюдения за их функционированием прекращаются. Примерами могут служить системы локализации аварии, скажем, система аварийного расхолаживания реактора, система аварийного электроснабжения и т.п. Имеются объекты, у которых в течение короткого времени проверяется работоспособность и на этом функционирование прекращается. Так периодически производится опробование дизель-генераторов, после непродолжительной работы их отключают.

4. Необходимость оценки надежности различных систем до наступления отказов ее комплектующих элементов. В настоящее время ко всем системам энергоблоков АЭС, важных для безопасности, предъявляется требование периодической оценки их надежности.

5. Наличие периодического контроля за исправностью функционирования объектов приводит к поступлению информации в отдельные моменты времени на границах интервалов наблюдений. Таким образом, наблюдателю не известно, как ведут себя объекты внутри интервала наблюдения; известными становятся состояния объектов только в моменты контроля. Данная схема наблюдений называется цензурированием интервалом или группированные данные.

6. Ненадежность устройств контроля, которые должны фиксировать отказы отдельных приборов или каналов. Это приводит к тому, что отказы объектов или каналов, у которых, в свою очередь, отказало уст-

ройство контроля, выявляются в моменты проведения проверок. Например, отказы обнаруживаются во время проведения ППР.

Цензурирование для группы однотипных объектов может быть задано в одной точке; с другой стороны, могут наблюдаться реализации, когда цензурирование проводится в разных точках. Примером первого случая цензурирования может служить план испытаний [N, U, 7] или [N, U, г] [38]. При плане [N, U, 7] наблюдения производят за TV объектами, длительность наблюдений равна Т единиц времени. По истечении этого времени испытания прекращаются не зависимо от того, сколько элементов отказало. Если отказало тп из N объектов, то для оставшихся (N— гп) объектов время наблюдения будет цензурировано величиной Т, т.е. известно, что на интервале [О, Т] (N - т) объектов не отказало и, вероятно, их отказы произойдут на интервале (Т, оо].

При плане [N, U, г] наблюдения производят за N объектами. Испытания прекращают тогда, когда откажет г объектов. В этом случае цен-зурирующим моментом является Т - момент отказа r-го объекта. Отказы остальных N— г изделий произойдут в интервале [7*, °°]. Такое цензурирование называется однократным.

Когда цензурирование производится в разных точках, оно называется многократным. Цензурирование может быть случайным и неслучайным. Цензурирование будет неслучайным тогда, когда цензуриру-ющие моменты у. детерминированы. Например, заранее спланированы моменты времени, в которые начинается профилактика. Примером неслучайного цензурирования являются результаты наблюдения за функционированием объектов, которые проходят испытания по плану [N, U, 7], когда момент Постановки испытаний известен заранее. При случайном цензурировании цензурирующие моменты у. являются реализациями случайной величины. Примером выборки со случайным цензурированием являются результаты наблюдений за испытанием объектов по плану [N, U, г]. Здесь момент приостановки наблюдений Г является случайной величиной и определяется моментом отказа r-го объекта.