Разбиение
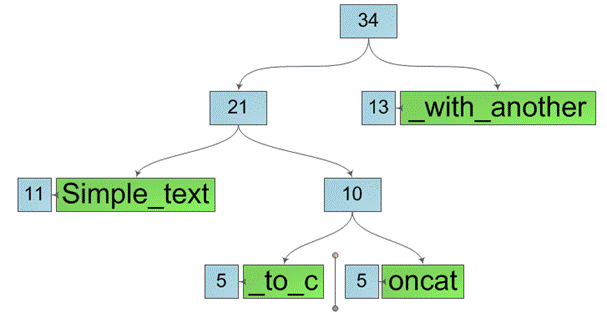
Место «разрыва» строки всегда находится в одном из листьев дерева. Разобьем этот лист на два новых, содержащих подстроки исходного листа. Причем для этой операции нам не понадобится копировать содержимое листа в новые, просто введем такие характеристики листа как offset и length и сохраним в новых листах указатели на массив символов исходного, изменив лишь смещение и длину:
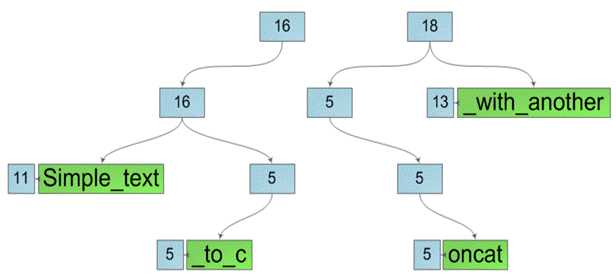
Далее будем расщеплять все узлы на пути от листа к корню, создавая вместо них пары узлов, принадлежащих, соответственно, левой и правой создаваемой подстроке. Причем мы опять же никак не изменяем текущий узел, а лишь создаем вместо него два новых. Это значит операция разделения строки порождает новые подстроки, не затрагивая исходную. После расщепления исходной строки мы получим две новые строки, как на рисунке ниже.
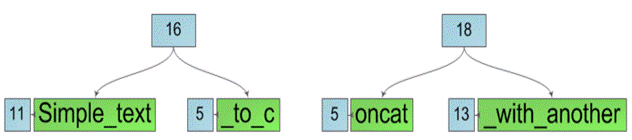
Нетрудно заметить что внутренняя структура таких строк не оптимальна — некоторые явно лишние. Однако исправить это досадное упущение легко — достаточно в обоих подстроках пройтись от места разреза к корню, заменяя каждый узел, имеющий ровно одного потомка этим самым потомком. После этого все лишние узлы пропадут и мы получим требуемые подстроки в их конечном виде:
Сложность же операции разбиения строк составляет, очевидно, О(h).
|