Нелинейная теплопроводность
Одним из актуальных направлений современной математической физики является изучение нелинейных математических моделей различных физико-химических явлений и процессов. Появление таких моделей обусловлено использованием в современной физике и технике воздействий на вещество электрических полей большой интенсивности, пучков частиц высокой энергии, мощного лазерного когерентного излучения, ударных волн высокой интенсивности, мощных тепловых потоков. Линейные математические модели являются всегда лишь определенными приближениями при описании различных процессов. Их можно использовать только в тех случаях, когда исследуемые физические величины в рассматриваемом процессе изменяются не в очень широком диапазоне значений. Нелинейные модели позволяют описать процессы в более широком диапазоне изменения параметров. При этом нелинейности изменяют не только количественные характеристики процессов, но и качественную картину их протекания. В основе нелинейных моделей лежат нелинейные дифференциальные уравнения в частных производных, законченной теории и общих методов решения задач для которых в настоящее время не разработано. Однако для ряда нелинейных задач математической физики удается найти точные аналитические решения, анализ свойств которых позволяет выявить качественно новые нелинейные эффекты в исследуемых процессах. В частности, при исследовании высокотемпературных тепловых процессов с учетом действия таких механизмов переноса энергии, как электронная или лучистая теплопроводности, необходимо учитывать зависимость плотности р, удельной теплоемкости с и коэффициента теплопроводности среды k от температуры. Мощность тепловых источников, распределенных в объеме среды, также может зависеть от температуры, если учитывать процессы диссоциации и ионизации молекул, фазовые переходы, излучение, горение, химические реакции и другие экзо- и эндотермические процессы, протекающие в нагретой среде. 2.1 Теория нелинейной теплопроводности Уравнение теплопроводности, учитывающее зависимость свойств среды от температуры и нелинейную зависимость от температуры мощности распределенных в объеме тепловых источников, является квазилинейным параболическим уравнением вида Нелинейность задачи теплопроводности может быть также обусловлена нелинейностью граничного условия. Такие задачи, в отличие от задач с внутренней нелинейностью, обусловленной нелинейностью уравнения, часто называют задачами с внешней нелинейностью. Нелинейное граничное условие на поверхности тела может иметь вид К таким условиям, например, относится условие на поверхности излучающего тела или условие конвективного теплообмена, в котором коэффициент теплообмена ат зависит от температуры поверхности тела. Задача теплопроводности становится нелинейной, если учитывать фазовые переходы в среде, такие, как плавление, испарение, конденсация, кристаллизация, происходящие при определенной температуре и сопровождающиеся выделением или поглощением теплоты. В среде с фазовым переходом появляется поверхность ∑ раздела фаз, которую называют фронтом фазового перехода. Эта поверхность перемещается с конечной скоростью. Баланс тепловой энергии на фронте фазового перехода с температурой u* позволяет записать на движущейся поверхности ∑ фронта кроме условия u1(P)=u2(P)=u*(1.3) другое граничное условие:
где k1, k2 и и1, u2 - коэффициенты теплопроводности и температуры двух соприкасающихся фаз соответственно; q* - удельная массовая теплота фазового перехода; V - мгновенная скорость перемещения фронта фазового перехода в направлении нормали Так как скорость перемещения фронта V заранее не известна и должна быть найдена в процессе решения задачи теплопроводности, то граничное условие (1.4), называемое условием Стефана, делает задачу нелинейной. Возможен и другой подход к моделированию процесса фазового перехода без явного выделения фронта фазового перехода при постановке задачи. Этот подход связан с переходом в класс обобщенных функций. Действительно, теплоту фазового перехода, выделяющуюся на фронте, можно учесть, считая внутреннюю энергию среды разрывной функцией температуры и вводя сосредоточенную теплоемкость среды. При этом внутренняя энергия единицы объема среды е, как функция температуры, при u = u* скачком изменяется на величину теплоты фазового перехода, т.е.
Здесь Q*=pq*; импульсная функция Хевисайда, производная которой
|

 (1.1)
(1.1)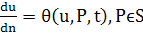 (1.2), где функция в нелинейным образом зависит от температуры.
(1.2), где функция в нелинейным образом зависит от температуры.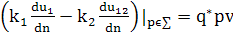 (1.4)
(1.4) поверхности∑;.
поверхности∑;. (1.5)
(1.5) = р(u) с(u) - теплоемкость единицы объема среды;
= р(u) с(u) - теплоемкость единицы объема среды;
 есть дельта-функция
есть дельта-функция .
.


