Пример 12.2
Выполнить деление Решение:
Для тригонометрической формы комплексного числа формула деления имеет вид
При делении комплексных чисел их модули, соответственно, делятся, а аргументы, соответственно, вычитаются. 15. Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.Обычно используется одно из следующих обозначений: Определение.Скалярным произведением в векторном пространстве для любых трех элементов для любых для любого Из определения скалярного произведения следует, что Свойства скалярного произведения: 16. Любая прямая на плоскости может быть задана уравнением первого порядкаАх + Ву + С = 0,причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 ¹ 0. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи: - C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат - А = 0, В ¹ 0, С ¹ 0 { By + C = 0}- прямая параллельна оси Ох - В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0} – прямая параллельна оси Оу - В = С = 0, А ¹ 0 – прямая совпадает с осью Оу - А = С = 0, В ¹ 0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий . 1. Общее уравнение прямой: Ax + By + C = 0. (2,1) 2. Уравнение прямой с угловым коэффициентом: y - y0 = k (x - x0), (2.2)
где k - угловой коэффициент прямой, то есть k = tgα, где α - величина угла, образованного прямой с осью Оx, M (x0, y0) - некоторая точка, принадлежащая прямой. Уравнение (2.2) принимает вид y = kx + b, если M (0, b) есть точка пересечения прямой с осью Оy.
3. Уравнение прямой в отрезках: x/a + y/b = 1 (2.3) где a и b - величины отрезков, отсекаемых прямой на осях координат. 4. Уравнение прямой, проходящей через две данные точки - A(x1, y1) и B(x2, y2): (2.4) 5. Уравнение прямой, проходящей через данную точку A(x1, y1) параллельно данному вектору a(m, n): (2.5) Нормальное уравнение прямой: rn0 - р = 0, (2.6) где r - радиус-вектор произвольной точки M(x, y) этой прямой, n0 - единичный вектор, ортогональный этой прямой и направленный от начала координат к прямой; р - расстояние от начала координат до прямой. Нормальное уравнение прямой в координатной форме имеет вид: x cosα + y sinα - р = 0, где α - величина угла, образованного прямой с осью Оx. Уравнение пучка прямых с центром в точке А(x1, y1) имеет вид: y-y1 = λ(x-x1), где λ - параметр пучка.
Взаимное расположение двух прямых на плоскости. Этот вопрос уже обсуждался в предыдущей лекции, когда оба уравнения данных прямых записывались в каноническом или параметрическом виде. Пусть сейчас оба уравнения прямых записаны в общем виде. Теорема. Пусть 1) если
2) если
3) если Вектор n(А,В) ортогонален прямой, числа A и B одновременно не равны нулю.
Основные задачи на прямую в пространстве
Прямая линия в пространстве. Основные формулы:
1. Канонические уравнения прямой линии в пространстве, или уравнения прямой с направляющими коэффициентами, имеют вид
где x0, y0, z0 - координаты точки, через которую проходит прямая, а m, n и p - направляющие коэффициенты прямой, которые являются проекциями на координатные оси Ox, Oy, Oz направляющего вектора прямой. Если
2. В параметрическом виде уравнения прямой линии в пространстве записываются так: x = x0 + mt; y = y0 + nt; z = z0 + pt, (4) где t - параметр. 3. Общие уравнения прямой:
Каждое из уравнений (5) - уравнение плоскости, и таким образом прямая в пространстве может рассматриваться как пересечение двух плоскостей, причем плоскости эти предполагаются непараллельными, т. е. соотношение 4. Условие параллельности двух прямых в пространстве: (6)
имеет вид 5. Условие перпендикулярности двух прямых (6) имеет вид mm1 + nn1 + pp1 = 0. (8) 6. Угол между двумя прямыми (6) определяется по формуле
(9)
7. Уравнение прямой, проходящей через две данные точки A(x1, y1, z1) и B(x2, y2, z2), запишутся в виде
(10)
17. Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом. Общее уравнение окружности записывается как: где Точка Уравнение окружности, проходящей через три точки (с помощью определителя)
Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F1 и F2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть | F1M | + | F2M | = 2a, причем | F1F2 | < 2a. Каноническое уравнение Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Гипе́рбола (др.-греч. ὑπερβολή, от др.-греч. βαλειν — «бросать», ὑπερ — «сверх») — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно. Точнее, причем | F1F2 | > 2a > 0.
Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы. Канонический вид
Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду ,где большая a и малая b полуоси. Пара́бола ( греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом Каноническое уравнение параболы в прямоугольной системе координат: (или
Приведение уравнения линии второго порядка к каноническому виду
Пусть в прямоугольной системе координат алгебраическая линия второго порядка задана уравнением (3.34): Чтобы привести уравнение к каноническому виду, нужно выполнить следующие действия. 1. Если в уравнении имеется член с произведением неизвестных
на угол а) переименование координатных осей: б) изменение направления координатной оси, например оси абсцисс: в) умножение обеих частей уравнения на отличный от нуля множитель; г) перенос членов из одной части уравнения в другую. В результате этих преобразований уравнение приводится к каноническому виду. Замену неизвестных, приводящую уравнение поверхности к каноническому виду, определяем как композицию всех замен, применяемых в ходе решения. 18. Всякая плоскость в пространстве определяется линейным уравнением
и обратно, всякое линейное уравнение (3) определяет плоскость в пространстве. Неполные уравнения плоскости:
А)
Б)
В) -
Г)
Д)
Е)
Ж)
Опр. Две плоскости в пространстве называются параллельными, если они не пересекаются, в противном случаи они пересекаются. Теорема1: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. Доказательство: Пусть и - данные плоскости, а1 и а2 - прямые в плоскости, пересекающиеся в точке А, в1 и в2 - соответственно параллельные им прямые в плоскости. Допустим, что плоскости и не параллельны, т.е. пересекаются по некоторой прямой с. По теореме прямые а1 и а2, как параллельные прямым в1и в2, параллельны плоскости, и поэтому они не пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости через точку А проходят две прямые (а1 и а2), параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию ЧТД. Перпендикулярные плоскости: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым. Теорема2: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. Доказательство:Пусть - плоскость, в -перпендикулярная ей прямая, - плоскость, проходящая через прямую в, с - прямая, по которой пересекаются плоскости и. Докажем, что плоскости и перпендикулярны. Проведем в плоскости через точку пересечения прямой в с плоскостью прямую а,перпендикулярную прямой с. Проведем через прямые а и в плоскость. Она перпендикулярна прямой с, т.к. прямая с перпендикулярна прямым а и в. Т. к. прямые а и в перпендикулярны, то плоскости и перпендикулярны. ч.т.д. 19. Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.
Итак, если уравнения двух непараллельных плоскостей
(11.11)И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему. Уравнения (11.11) называют общими уравнениями прямой в пространстве. Замечание 11.2 Любые попытки с помощью преобразований уравнений системы (11.11) получить одно (линейное) уравнение, задающее прямую, обречены на неудачу. Одно уравнение -- это уравнение плоскости. Общие уравнения прямой "неудобны" для получения информации о положении прямой. Например, чтобы найти координаты какой-нибудь точки на прямой, нужно провести довольно сложные вычисления. А именно, задать произвольно какую-нибудь координату, подставить ее в систему (11.11) и из получившейся системы двух уравнений с двумя неизвестными найти две остальные координаты. Причем может оказаться, что полученная система не имеет решений. Тогда нужно произвольно задать другую координату и из системы найти две оставшиеся координаты.
|



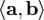 .
. 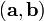 .
. 
 над полем
над полем  называется функция
называется функция  для элементов
для элементов  , принимающая значения в
, принимающая значения в  и
и  пространства
пространства  справедливо равенство
справедливо равенство  (линейность скалярного произведения по первому аргументу);
(линейность скалярного произведения по первому аргументу); и
и  , где черта означает комплексное сопряжение (эрмитова симметричность);
, где черта означает комплексное сопряжение (эрмитова симметричность); , причем только при
, причем только при  (положительная определенность скалярного произведения).Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.Заметим, что из п.2 определения следует, что
(положительная определенность скалярного произведения).Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.Заметим, что из п.2 определения следует, что  действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.
действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.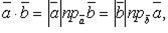 где, например,
где, например,  есть величина проекции вектора
есть величина проекции вектора 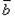 на направление вектора
на направление вектора 


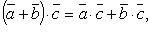


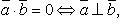

 и
и  – общие уравнения двух прямых на координатной плоскости Оху. Тогда
– общие уравнения двух прямых на координатной плоскости Оху. Тогда , то прямые
, то прямые  и
и 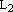 совпадают;
совпадают; , то прямые
, то прямые  , то прямые
, то прямые 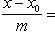
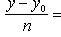
 (1)
(1) ,
,  и -
и - 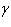 углы между прямой и координатными осями Ox, Oy и Oz, то
углы между прямой и координатными осями Ox, Oy и Oz, то 
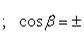
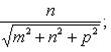

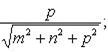 (2)
(2)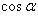 ,
,  и
и  называются направляющими косинусами прямой. Направляющие коэффициенты m, n и p можно рассматривать как проекции на координатные оси вектора, параллельного прямой, причем m, n и p не могут быть одновременно равны нулю. Уравнения (1) могут быть записаны также в виде
называются направляющими косинусами прямой. Направляющие коэффициенты m, n и p можно рассматривать как проекции на координатные оси вектора, параллельного прямой, причем m, n и p не могут быть одновременно равны нулю. Уравнения (1) могут быть записаны также в виде 

 (3)
(3)

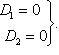 (5)
(5)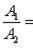

 не имеет места.
не имеет места.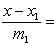

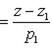


 (7)
(7)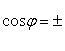
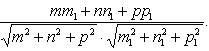
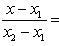
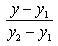


 отличен от нуля.
отличен от нуля.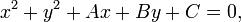 или
или 

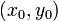 — центр окружности, R — её радиус.
— центр окружности, R — её радиус.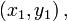
 и
и 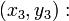
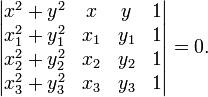



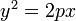
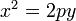 , если поменять местами оси).
, если поменять местами оси).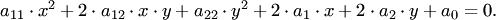
 , то делаем поворот системы координат:
, то делаем поворот системы координат: 
 , удовлетворяющий равенству
, удовлетворяющий равенству  . При этом получим "почти" приведенное уравнение линии второго порядка:
. При этом получим "почти" приведенное уравнение линии второго порядка:  Если
Если  , переходим к пункту 2, поворот системы координат делать не нужно, так как исходное уравнение имеет "почти" приведенный вид. 2. Выполняем параллельный перенос системы координат:а) если в уравнении нет линейных членов, то переходим к пункту 3;б) если в уравнении имеется линейный член с какой-либо неизвестной и квадратичный член с этой же неизвестной, то, дополняя эти члены до полного квадрата, делаем замену, чтобы в уравнении не стало линейного члена с этой неизвестной. Например, если в уравнении
, переходим к пункту 2, поворот системы координат делать не нужно, так как исходное уравнение имеет "почти" приведенный вид. 2. Выполняем параллельный перенос системы координат:а) если в уравнении нет линейных членов, то переходим к пункту 3;б) если в уравнении имеется линейный член с какой-либо неизвестной и квадратичный член с этой же неизвестной, то, дополняя эти члены до полного квадрата, делаем замену, чтобы в уравнении не стало линейного члена с этой неизвестной. Например, если в уравнении  и
и 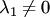 ,то выполняем преобразования:
,то выполняем преобразования: 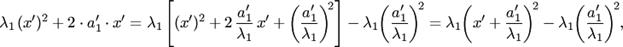 а затем замену неизвестных
а затем замену неизвестных  , после которой в уравнении не будет линейного члена с неизвестной
, после которой в уравнении не будет линейного члена с неизвестной  ; в) если в уравнении имеется только один линейный член с какой-либо неизвестной, а квадрат этой неизвестной отсутствует, то при помощи замены этой переменной надо сделать равным нулю свободный член уравнения. Например, если уравнение имеет вид
; в) если в уравнении имеется только один линейный член с какой-либо неизвестной, а квадрат этой неизвестной отсутствует, то при помощи замены этой переменной надо сделать равным нулю свободный член уравнения. Например, если уравнение имеет вид  то, выполняя замену неизвестных
то, выполняя замену неизвестных  , получаем уравнение без свободного члена:
, получаем уравнение без свободного члена:  енное в результате упрощений (пункт 2) уравнение имеет "почти" канонический вид. Для окончательного упрощения "почти" канонического уравнения при необходимости применяются следующие преобразования:
енное в результате упрощений (пункт 2) уравнение имеет "почти" канонический вид. Для окончательного упрощения "почти" канонического уравнения при необходимости применяются следующие преобразования: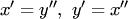 ;
; ;
;
 - уравнение плоскости, проходящей через начало координат;
- уравнение плоскости, проходящей через начало координат; - уравнение плоскости, параллельной оси;
- уравнение плоскости, параллельной оси; уравнение плоскости, параллельной оси;
уравнение плоскости, параллельной оси;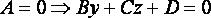 - уравнение плоскости, параллельной оси;
- уравнение плоскости, параллельной оси; - уравнение плоскости, параллельной координатной плоскости;
- уравнение плоскости, параллельной координатной плоскости; - уравнение плоскости, параллельной координатной плоскости;
- уравнение плоскости, параллельной координатной плоскости; - уравнение плоскости, параллельной координатной плоскости.
- уравнение плоскости, параллельной координатной плоскости.
 и
и  , то прямая, являющаяся их линией пересечения, задается системой уравнений
, то прямая, являющаяся их линией пересечения, задается системой уравнений 



