Г. Санкт-Петербург.

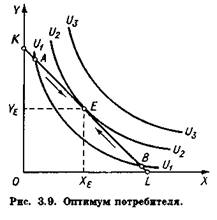
Какой товарный набор выберет потребитель? Из всех доступных для него наборов потребитель выберет тот, который принадлежит наиболее удаленной от начала координат кривой безразличия. Именно этот набор обеспечит ему максимум удовлетворения. Потребитель не выберет точку А, в которой бюджетная линия пересекает некоторую кривую безразличия, ведь при движении вдоль бюджетной линии вправо вниз потребитель может перейти к товарным наборам, лежащим на более удаленных от начала координат кривых безразличия. По аналогичным причинам потребитель не выберет точку В. Он выберет точку Е, в которой бюджетная линия лишь касается некоторой кривой безразличия U2- Оптимальный для потребителя товарный набор Е содержит Хе единиц товара X и Ye единиц товара У.

В точке Е наклоны бюджетной линии и кривой безразличия совпадают. Напомним, что наклон бюджетной линии равен ~Рх/Ру> наклон кривой безразличия равен —MRSxy- Поэтому в точке оптимума выполняется равенство

Условие оптимума потребителя (3.12) можно интерпретировать следующим образом. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим без изменения уровня своего удовлетворения.

Равенство (3.12) в порядковой теории полезности имеет такой же смысл, что и равенство (3.4) в количественной теории. Действительно, согласно (3.8),

Подставив (3.8) в (3.12), получаем условие оптимума потребителя в следующем виде:

Последнее равенство совпадает с равенством (3.4).

Оптимальное решение, представленное на рис. 3.9, называют часто внутренним, поскольку точка Е лежит внутри двумерного пространства товаров, точнее — его / квадранта. Однако в некоторых ситуациях бюджетная прямая и кривая безразличия имеют разный наклон на всем их протяжении и, значит, точки касания их вообще не существует. В этом случае оптимальное решение определяется положением, наиболее близким к касанию, и называется угловым. Оно определяется пересечением бюджетной прямой, одной из осей координат и кривой безразличия.

На рис. 3.10 бюджетная прямая KL ограничена точками К, где X = 0, и L, где У = 0. Оптимум потребителя достигается либо в точке К (рис. 3.10,а), если

В первом случае наклон кривой безразличия в точке К меньше или равен наклону бюджетной прямой, во втором наклон кривой безразличия в точке L больше или равен наклону бюджетной прямой.

Из всех доступных потребителю наборов набор К (рис. З.Ю.а) и набор L (рис. 3.10,6) лежат на наиболее удаленных от начала координат кривых безразличия. Набор К не содержит товара X, набор L — товара У. Естественно, для точек К и L условие (3.12) может и не выполняться. Угловое решение в порядковой теории полезности соответствует условию (3.5) в количественной теории.

 

г. Санкт-Петербург.