Как было показано в §2.3, в диэлектриках источниками поля кроме сторонних являются также и связанные заряды. Поэтому теорема Гаусса для  запишется:
запишется:
 . (2.24)
. (2.24)
Так как из (2.23)  , то:
, то:  . Тогда:
. Тогда:
 , или
, или
 . (2.25)
. (2.25)
Если ввести вектор  , то электрическая индукция
, то электрическая индукция  измеряется в тех же единицах, что и
измеряется в тех же единицах, что и  , т.е. в Кл/м2,
, т.е. в Кл/м2,  - В/м, и из (2.25) получим:
- В/м, и из (2.25) получим:
 . (2.26)
. (2.26)
Это теорема Гаусса для вектора  .
.
Поток вектора  через замкнутую поверхность равен стороннему заряду, заключенному внутри этой поверхности.
через замкнутую поверхность равен стороннему заряду, заключенному внутри этой поверхности.
Видно, что единственным источником  являются свободные заряды. Вектор
являются свободные заряды. Вектор  начинается на
начинается на  и заканчивается на
и заканчивается на  .
.
Учтем, что:  (2.19), тогда:
(2.19), тогда:
 , (2.27)
, (2.27)
 - (2.28)
- (2.28)
диэлектрическая проницаемость.
Применив (2.26) для точечного заряда, получим:
 ;
;  .
.
 . (2.29)
. (2.29)
Если учесть, что  , то напряженность поля точечного заряда в диэлектрике:
, то напряженность поля точечного заряда в диэлектрике:
 , (2.30)
, (2.30)
то есть внутри диэлектрика поле в  раз меньше, чем в вакууме. Именно с рассмотрения вопроса, почему поле в диэлектрике меньше, чем внешнее (или поле в вакууму) и начиналось изучение электрического поля в диэлектрике (§2.3). Отсюда ясен физический смысл
раз меньше, чем в вакууме. Именно с рассмотрения вопроса, почему поле в диэлектрике меньше, чем внешнее (или поле в вакууму) и начиналось изучение электрического поля в диэлектрике (§2.3). Отсюда ясен физический смысл  . Во столько же раз меньше и потенциал точечного заряда:
. Во столько же раз меньше и потенциал точечного заряда:
 . (2.31)
. (2.31)
Тогда, емкость конденсатора при наличии диэлектрика в  раз больше емкости, между пластинами которой содержится вакуум.
раз больше емкости, между пластинами которой содержится вакуум.
Рассмотрим теперь граничные условия для  на границе двух диэлектриков.
на границе двух диэлектриков.
 На границе двух диэлектриков (рис.2.14) в поле
На границе двух диэлектриков (рис.2.14) в поле  возникают связанные заряды. Имеются две границы – 1-2 и 2-1 и две нормали на границе
возникают связанные заряды. Имеются две границы – 1-2 и 2-1 и две нормали на границе  и
и  . Они и показывают, какую границу мы рассматриваем.
. Они и показывают, какую границу мы рассматриваем.
1. Рассмотрим границу 1-2 (рис.2.15). Нормаль  положительна, при этом
положительна, при этом  (например, воздух-диэлектрик).
(например, воздух-диэлектрик).
 Чтобы вывести условия для нормальных составляющих, используем теорему Гаусса. В качестве замкнутой поверхности рассмотрим цилиндр (рис.2.15), для которого:
Чтобы вывести условия для нормальных составляющих, используем теорему Гаусса. В качестве замкнутой поверхности рассмотрим цилиндр (рис.2.15), для которого:
 ,
,  .
.
Тогда из (2.23),  - связанные заряды.
- связанные заряды.
 , (2.32)
, (2.32)
но так как  , то из (2.19) следует, что:
, то из (2.19) следует, что:
 ,
,  .
.
Тогда  , что и видно из рис.2.14.
, что и видно из рис.2.14.
Если  , т.е. на границе нет сторонних зарядов, то, применив (2.26) и (2.24), получим:
, т.е. на границе нет сторонних зарядов, то, применив (2.26) и (2.24), получим:
 , (2.33)
, (2.33)
 . (2.34)
. (2.34)
Но так как  , то
, то  . Это согласуется с результатами для
. Это согласуется с результатами для  . С учетом знака
. С учетом знака  для границы 1-2 запишем граничные условия (2.32-2.34):
для границы 1-2 запишем граничные условия (2.32-2.34):
 ,
,
 ,
,
 .
.
Так как  , то:
, то:
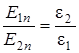 . (2.35)
. (2.35)
2. Рассмотрим границу 2-1 (рис.2.16):  .
.
 Используя теорему Гаусса как и на границе 1-2 и учтя, что
Используя теорему Гаусса как и на границе 1-2 и учтя, что  ,
,  , получим:
, получим:
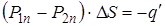 ;
;
 ;
;  ;
;
Тогда:  ; при этом
; при этом  , что согласуется с рис.2.14. Чтобы найти тангенциальные составляющие, используем теорему о циркуляции вектора
, что согласуется с рис.2.14. Чтобы найти тангенциальные составляющие, используем теорему о циркуляции вектора  (1.27). Выбрав контур в виде прямоугольника абвг, получим условие для
(1.27). Выбрав контур в виде прямоугольника абвг, получим условие для  .
.

 ;
;
 ;
;
 . (2.36)
. (2.36)
Подставляя выражения для  и
и 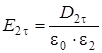 , получим:
, получим:
 . (2.37)
. (2.37)
При 
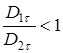

 ;
;  .
.
Преломление силовых линий на границе.
Возьмем, как и прежде  , тогда: из (2.35) и (2.36):
, тогда: из (2.35) и (2.36):
 ,
,  ,
,
а также из (2.32):
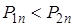 ,
,  ,
,
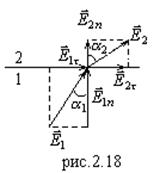
Поэтому углы  (см. рис.2.18).
(см. рис.2.18).
Тогда  , т.к.
, т.к.
 . (2.38)
. (2.38)
Силовые линии поля ведут себя, как показано на рис.2.18, т.е. преломляются на границе.
Пример.
 Точечный заряд
Точечный заряд 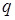 находится в центре шара из диэлектрика с проницаемостью
находится в центре шара из диэлектрика с проницаемостью  . Радиус шара
. Радиус шара  . Шар окружен безграничным диэлектриком с проницаемостью
. Шар окружен безграничным диэлектриком с проницаемостью  (рис.2.19). Найти
(рис.2.19). Найти  на границе диэлектрика и связанный заряд внутри шара.
на границе диэлектрика и связанный заряд внутри шара.
Напряженность поля как функция расстояния  от центра шара по теореме Гаусса для
от центра шара по теореме Гаусса для  (2.26) и формуле (2.27) запишем:
(2.26) и формуле (2.27) запишем:
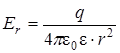 .
.
Тогда:
 ; и
; и
 . (2.39)
. (2.39)
На границе 1-2 между диэлектриками:
 . (2.40)
. (2.40)
Видим, что знак  зависит от соотношения между
зависит от соотношения между  и
и  . При
. При  ,
,  ,
,  ,
, 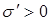 . Внутри шара при
. Внутри шара при  из (2.23):
из (2.23):
 .
.
Подставив (2.39), получим:
 . (2.41)
. (2.41)
Видно, что внутри шара всегда появляется связанный заряд  , если заряд
, если заряд  .
.
Звоните и приезжайте
Содержание 1 2 3

 запишется:
запишется: . (2.24)
. (2.24) , то:
, то:  . Тогда:
. Тогда: , или
, или . (2.25)
. (2.25) , то электрическая индукция
, то электрическая индукция  измеряется в тех же единицах, что и
измеряется в тех же единицах, что и  , т.е. в Кл/м2,
, т.е. в Кл/м2,  . (2.26)
. (2.26) и заканчивается на
и заканчивается на  .
. (2.19), тогда:
(2.19), тогда: , (2.27)
, (2.27) - (2.28)
- (2.28) ;
;  .
. . (2.29)
. (2.29) , то напряженность поля точечного заряда в диэлектрике:
, то напряженность поля точечного заряда в диэлектрике: , (2.30)
, (2.30) раз меньше, чем в вакууме. Именно с рассмотрения вопроса, почему поле в диэлектрике меньше, чем внешнее (или поле в вакууму) и начиналось изучение электрического поля в диэлектрике (§2.3). Отсюда ясен физический смысл
раз меньше, чем в вакууме. Именно с рассмотрения вопроса, почему поле в диэлектрике меньше, чем внешнее (или поле в вакууму) и начиналось изучение электрического поля в диэлектрике (§2.3). Отсюда ясен физический смысл  . (2.31)
. (2.31) на границе двух диэлектриков.
на границе двух диэлектриков. На границе двух диэлектриков (рис.2.14) в поле
На границе двух диэлектриков (рис.2.14) в поле  и
и  . Они и показывают, какую границу мы рассматриваем.
. Они и показывают, какую границу мы рассматриваем. (например, воздух-диэлектрик).
(например, воздух-диэлектрик). Чтобы вывести условия для нормальных составляющих, используем теорему Гаусса. В качестве замкнутой поверхности рассмотрим цилиндр (рис.2.15), для которого:
Чтобы вывести условия для нормальных составляющих, используем теорему Гаусса. В качестве замкнутой поверхности рассмотрим цилиндр (рис.2.15), для которого: ,
,  .
. - связанные заряды.
- связанные заряды. , (2.32)
, (2.32) , то из (2.19) следует, что:
, то из (2.19) следует, что: ,
,  .
. , что и видно из рис.2.14.
, что и видно из рис.2.14. , т.е. на границе нет сторонних зарядов, то, применив (2.26) и (2.24), получим:
, т.е. на границе нет сторонних зарядов, то, применив (2.26) и (2.24), получим: , (2.33)
, (2.33) . (2.34)
. (2.34) , то
, то  . С учетом знака
. С учетом знака  для границы 1-2 запишем граничные условия (2.32-2.34):
для границы 1-2 запишем граничные условия (2.32-2.34): ,
, .
. , то:
, то: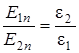 . (2.35)
. (2.35) .
. Используя теорему Гаусса как и на границе 1-2 и учтя, что
Используя теорему Гаусса как и на границе 1-2 и учтя, что  ,
,  , получим:
, получим: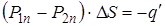 ;
; ;
;  ;
; ; при этом
; при этом  , что согласуется с рис.2.14. Чтобы найти тангенциальные составляющие, используем теорему о циркуляции вектора
, что согласуется с рис.2.14. Чтобы найти тангенциальные составляющие, используем теорему о циркуляции вектора  .
.
 ;
; ;
; . (2.36)
. (2.36) и
и 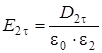 , получим:
, получим: . (2.37)
. (2.37)
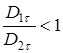

 ;
;  .
.
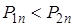 ,
,  (см. рис.2.18).
(см. рис.2.18). , т.к.
, т.к. . (2.38)
. (2.38) Точечный заряд
Точечный заряд 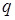 находится в центре шара из диэлектрика с проницаемостью
находится в центре шара из диэлектрика с проницаемостью  . Радиус шара
. Радиус шара  . Шар окружен безграничным диэлектриком с проницаемостью
. Шар окружен безграничным диэлектриком с проницаемостью  (рис.2.19). Найти
(рис.2.19). Найти  на границе диэлектрика и связанный заряд внутри шара.
на границе диэлектрика и связанный заряд внутри шара. от центра шара по теореме Гаусса для
от центра шара по теореме Гаусса для 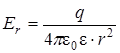 .
. ; и
; и . (2.39)
. (2.39) . (2.40)
. (2.40) ,
,  ,
, 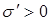 . Внутри шара при
. Внутри шара при  из (2.23):
из (2.23): .
. . (2.41)
. (2.41) , если заряд
, если заряд 


