Теоретическая часть. Вынужденные колебания в линейной диссипативной системе при гармоническом внешнем воздействии описываются дифференциальным уравнением
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Вынужденные колебания в линейной диссипативной системе при гармоническом внешнем воздействии описываются дифференциальным уравнением
где Р0 – амплитуда внешней силы, р – частота внешней силы, d - коэффициент затухания, w0 – частота собственных колебаний. Система (1) является линейной, так как все параметры постоянны. Общее решение этого уравнения имеет вид:
А и В определяются из начальных условий. С течением времени собственное колебание, описываемое первым слагаемым в выражении (2) затухает, и в системе устанавливается вынужденное колебание, амплитуда
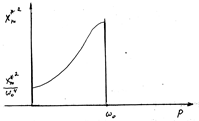
Резонансные кривые для разных коэффициентов затухания, изображенные на рис.1, соответствуют установившемуся стационарному процессу и определяют зависимость амплитуды колебаний от частоты внешней силы.
Рис. 1. Максимальная амплитуда колебаний достигается не при точном совпадении собственной частоты колебаний с частотой вынуждающей силы (как в случае консервативной системы), а смещается влево по оси частот на величину, зависящую от d. Максимум К характерным свойствам вынужденных колебаний в линейной системе можно отнести следующие: 1. частота колебаний совпадает с частотой вынуждающей силы; 2. так как в линейной системе действует принцип суперпозиции, увеличение амплитуды внешней силы в несколько раз дает увеличение амплитуды колебаний во столько же раз. Если какой-либо из параметров колебательной системы не является постоянным, а определяется свойствами системы, то уравнение (1) становится нелинейным. Общий вид уравнения, описывающего вынужденные колебания в нелинейной системе
Рассмотрим колебательные процессы, происходящие в системе под действием внешней гармонической силы
Положим Тогда уравнение вынужденных колебаний принимает вид
Вынужденные колебания в нелинейной системе происходят не только на частоте внешней силы, но и на ее гармониках и субгармониках, то есть должны существовать и колебания частот 2р, 3р и т.д. Однако при достаточно высокой добротности системы и условии, что р»
где Амплитуда рассматриваемых колебаний определяется из решения системы уравнений (5) и (6).
Резонансные кривые (зависимость А(р)) для разных значений амплитуды внешней силы изображены на рис. 2(а, б). Штриховой линией изображена зависимость  для симметричной нечетной f(x) (опорная кривая). для симметричной нечетной f(x) (опорная кривая).
Рис. 2. Отметим основные особенности резонанса в нелинейной системе: 1. Резонансные кривые в силу неизохронности наклонены и могут быть двух видов: а. Монотонные кривые (для б. Другой вид резонансных кривых соответствует амплитудам внешней силы, большим F0крит. В этом случае у резонансных кривых имеются участки с неоднозначной зависимостью амплитуды А от частоты внешнего воздействия. В области частот, где резонансная кривая трехзначна, среднее значение амплитуды неустойчиво (участок ЕС), поэтому при экспериментальном исследовании наблюдаются скачки амплитуды при достижении границ неустойчивой области.
2. Изменение амплитуды А с изменением частоты в разных направлениях происходит по-разному. Если снимать АЧХ в сторону увеличения частоты (от Если частоту менять в обратном направлении, то скачок амплитуды (резкое увеличение) происходит уже при В данном случае рассмотрена жесткая система (g>0). При g<0 (мягкая система) кривые будут иметь наклон в противоположную сторону. Для другого вида f(x) зависимость В системах с нелинейными потерями изменение амплитуды колебаний не влияет на собственную частоту. Поэтому резонансные кривые не имеют наклона. Характерной особенностью зависимости А(р) является наличие более плоской вершины резонансной кривой (в сравнении с линейной диссипацией).
|


 , (1)
, (1) (2)
(2)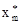 и начальная фаза
и начальная фаза 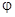 которого определяются выражениями
которого определяются выражениями
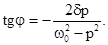 (3)
(3)

 имеет место при
имеет место при  .
.
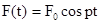 , когда нелинейной является возвращающая сила
, когда нелинейной является возвращающая сила .
.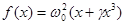 (такое приближение верно при нечетной характеристике возвращающей силы и не слишком больших х; предполагается, что
(такое приближение верно при нечетной характеристике возвращающей силы и не слишком больших х; предполагается, что  ).
). . (4)
. (4)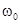 гармоники выражены слабо, и решение уравнения (4) можно искать в виде
гармоники выражены слабо, и решение уравнения (4) можно искать в виде  Подставляя это решение в (4) и отбрасывая гармоники (метод гармонического баланса), получаем
Подставляя это решение в (4) и отбрасывая гармоники (метод гармонического баланса), получаем
 , (5)
, (5)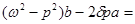 0, (6)
0, (6) - частота собственных колебаний нелинейной системы (4). Характерным является тот факт, что частота собственных колебаний зависит от амплитуды колебаний
- частота собственных колебаний нелинейной системы (4). Характерным является тот факт, что частота собственных колебаний зависит от амплитуды колебаний  . Такие колебания в системе с нелинейной возвращающей силой называются неизохронными.
. Такие колебания в системе с нелинейной возвращающей силой называются неизохронными.

 ) характеризуется однозначной зависимостью амплитуды вынужденных колебаний от частоты внешней силы и представляют собой несколько деформированные резонансные кривые для обычной линейной системы. Максимум их смещен в сторону бо¢льших частот в соответствии с выражением для
) характеризуется однозначной зависимостью амплитуды вынужденных колебаний от частоты внешней силы и представляют собой несколько деформированные резонансные кривые для обычной линейной системы. Максимум их смещен в сторону бо¢льших частот в соответствии с выражением для  при
при  (рис. 2а).
(рис. 2а). ), то амплитуда изменяется сначала по кривой АВС. При
), то амплитуда изменяется сначала по кривой АВС. При  амплитуда скачком уменьшается и далее меняется монотонно по кривой DF.
амплитуда скачком уменьшается и далее меняется монотонно по кривой DF. . Участок EC экспериментально не может быть получен, так как соответствующие ему режимы неустойчивы.
. Участок EC экспериментально не может быть получен, так как соответствующие ему режимы неустойчивы.


