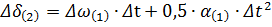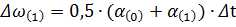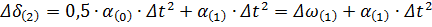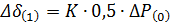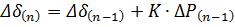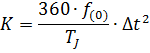Метод последовательных интервалов.
В клініку поступив хворий К, 50 років з скаргами на гостру біль в правому підребер’ї, блювота по типу «кофейна гуща». Шкіра бліда, хворий загальмований. Об’єктивно: Пульс – 96 уд. за хв., частий, слабко наповнення, АТ-85/40 мм рт/ст. В анамнезі виразкова хвороба шлунку. Неодноразово проводив консервативне лікування в гастроентерологічному відділенні. Дієти не притримувався. Професія авіадиспетчер. При пальпації живіт м’який, болючий в епігастральній ділянці і проекції жовчного міхура. При пальпації кишковика не виявляється його чутливість в проекції сигмовидної кишки. Стілець і сечовиділення відсутні. Питання: 1. Про який діагноз необхідно подумати? 2. Які методи обстеження потрібно призначити хворому? 3. Тактика лікування в критичній ситуації. Лекция №8. Метод последовательных интервалов. Является упрощенным решением дифференциального уравнения описывающего вращение ротора генератора. Решением этого уравнения является зависимость угла δ от времени при переходном электромеханическом процессе. Уравнение относительного движения синхронной машины при небалансе момента турбины и электромагнитного момента может быть записано в следующем виде:
Где Решение записанного уравнения означает определение зависимости При расчетах относительного движения ротора, происходящего со скоростью много меньше синхронной, полагают, что мощность численно равна моменту. Тогда:
В методе последовательных интервалов, предполагают, что задача уже решена и подлежащие нахождению зависимости изображаются в следующем виде:
Частота вращения ротора генератора записывается в виде:
Производная по времени от относительной скорости вращения ротора равна ускорению ротора: Производная по времени от угла δ это есть относительная скорость вращения ротора генератора:
Следствием этих выражений является запись:
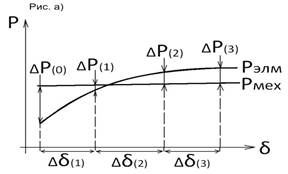
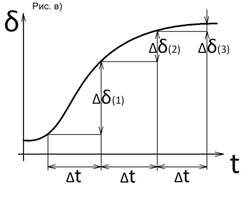
Разобьем весь процесс на малые интервалы времени Δt и будем рассматривать его последовательно от интервала к интервалу. Выбирая одинаковые интервалы по времени (рис. б и в) будем иметь неодинаковые интервалы по углу (рис. а). Каждый интервал характеризуется определенными значениями начальных и конечных величин угла, скорости, ускорения и средними значениями скорости и ускорения действующими в данном интервале. Начальные значения этих величин в последних интервалах выбирают такой, чтобы на его протяжении можно было считать ускорение неизменным. Обычно Δt =0,02-0,1 сек. В первом интервале начальная скорость равна нулю, и при постоянном ускорении равна α (рис.б) изменение угла будет происходить по закону равноускоренного движения. Приращение угла к концу интервала составит
Приращение мощности
Соответственно во втором интервале изменение угла δ зависит от скорости Приращение угла δ во втором интервале:
Значение скорости на протяжении первого интервала непостоянно, ее среднее значение определяется:
Тогда Аналогично получаются выражения для приращения угла в третьем, четвертом и последующих интервалах, которые записываются в следующем виде:
|

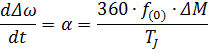
 ,
,  -постоянная инерции ротора.
-постоянная инерции ротора.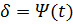 .
.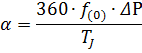

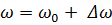 , где
, где 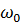 -синхронная скорость,
-синхронная скорость, 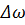 -угловая скорость относительного движения ротора (относительно синхронной).
-угловая скорость относительного движения ротора (относительно синхронной).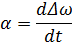
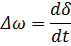

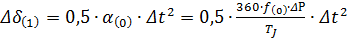
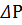 изменяется при изменениях угла и времени. Зная приращение Δt и приращение
изменяется при изменениях угла и времени. Зная приращение Δt и приращение 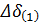 можно определить
можно определить 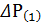 (по аналитической зависимости электрической мощности от угла) - небаланс мощности в конце первого или в начале второго интервала. В конце первого интервала мы нашли угол
(по аналитической зависимости электрической мощности от угла) - небаланс мощности в конце первого или в начале второго интервала. В конце первого интервала мы нашли угол 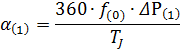
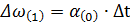 , которую получил ротор в первом интервале и ускорения
, которую получил ротор в первом интервале и ускорения 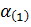 .
.