Метод случайного распределения

http://www.tecsun.com.cn

Схема контроля

Фамилия	Слева	Справа
Калинина
Карпова
Ламекина
Никонова
Плужников
Русак
Сафонова
Стернин
Филимонова
Воронов

 

А теперь самое весёлое, то что все просили объяснить!!!

 

Есть эффект последовательности. Предыдущие оценки влияют на последующие. Нужно сделать, чтоб позиция предъявления в ряду в последовательности проб у каждого объекта была одинаковая – позиционное уравнивание.

 

С помощью таблицы случайных чисел с равномерным распределением делаем. Таблица есть в яндексе и на почте. Каждой паре фамилии присваиваем число, взятое из таблице. Я брала 1- и 2х- значные числа подряд. В табличке ниже это 2 колонка.

 

Далее ранжируем. Это можно сделать вручную, я делала в программе Access. Он есть в винде. Жмём там создать новую базу данных, потом создание таблице в режиме конструктора. В первую колонку вбиваем пару фамилий, во вторую случайные числа.

Можно сохраниться на всякий случай. Потом жмём по колонке с числами правой кнопкой мыши и выбираем сортировку по возрастанию. Вуаля! Самая левая колонка – код – это и есть порядковые номера, они у меня в третьей колонке ниже. Собственно порядковые номера это и есть порядок предъявления карточек!

 

Есть только проблема. Я не знаю как переносить данные из ворда в аксес и эксель, поэтому вбивала вручную всё каждый раз=(

 

Метод случайного распределения

Пара фамилий	Случайные числа	Порядковый номер
1.Калинина – Карпова
2.Калинина – Ламекина
3.Калинина – Никонова
4.Калинина – Пужников
5.Калинина - Русак
6.Сафонова – Калинина
7.Стернин – Калинина
8.Филимонова – Калинина
9.Воронов – Калинина
10.Карпова – Ламекина
11.Карпова – Никонова
12.Карпова – Плужников
13.Карпова – Русак
14.Сафонова – Карпова
15.Стернин – Карпова
16.Филимонова – Карпова
17.Воронов – Карпова
18.Ламекина – Никонова
19.Ламекина – Плужников
20.Ламекина – Русак
21.Ламекина – Сафонова
22.Стернин – Ламекина
23.Филимонова – Ламекина
24.Воронов – Ламекина
25.Никонова – Плужников
26.Никонова – Русак
27.Никонова – Сафонова
28.Никонова – Стернин
29.Филимонова – Никонова
30.Воронов – Никонова
31.Плужников – Русак
32.Плужников – Сафонова
33.Плужников – Стернин
34.Плужников – Филимонова
35.Плужников – Воронов
36.Русак – Сафонова
37.Русак – Стернин
38.Русак – Филимонова
39.Русак – Воронов
40.Сафонова – Стернин
41.Сафонова – Филимонова
42.Сафонова – Воронов
43.Стернин – Филимонова
44.Стернин – Воронов
45.Филимонова – Воронов

 

 

Считаем среднюю позицию каждой фамилии. В идеале – 23, но это практически невозможно, не пугайтесь =)

Числа в числители - сумма всех позиций(3 колонка), на которых находится фамилия данного человека.

 

 

Средние позиции:

 

Калинина 7+6+34+12+14+35+23+1+16 = 16.4

Карпова 7 +24+36+37+44+39+15+33+17 = 28

 

Ламекина 6 +39+42+41+88+18+29+10+25 = 33.1

Никонова 34 +15+42+4+32+40+26+21+45 =28.7

Плужников 12 +33+41+4+11+38+27+20+19 =22.7

Русак 14 +17+88+32+11+9+31+30+3 =26.1

Сафонова 35 +24+18+40+38+9+2+5+22 =21.4

Стернин 23 +36+29+26+27+31+2+13+43 =25.5

Филимонова 1 +37+10+21+20+30+5+13+28 =18.3

Воронов 16 +44+25+45+19+3+22+43+28 =27.2

 

Сравнив самую большую среднюю позицию и самую маленькую, чтобы узнать существуют ли между ними значимые отличия. Используем критерий Стъюдента для сравнения двух средних. («несвязанных» совокупностей). Кстати, мы это на матметодах проходили, может у кого есть в тетради алгоритм, но я распишу.

 

Гипотезы

H0 – Между средними позициями объектов есть незначимые различия

H1 – Между средними позициями объектов есть значимые различия

 

t=

 

(в знаменателе под корнем ВСЁ!)

 

 

В числители собственно средние, полученные выше.

n – везде 9, это количество

S-это дисперсия. Её можно посчитать в экселе, как я и сделала, потому что это быстро или по формуле:

 

 

 

Итоговый результат:

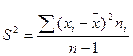
=596,1 (Ламекина)

 

=144,7 (Калинина)