Последовательный симплекс метод.
Этот метод относится к методам экспериментальной оптимизации. Он широко используется в производственной и лабораторной практике. Выбор этого метода планирования эксперимента определяется отсутствием требований к необходимости постановки большого количества опытов (план ненасыщенный) для составления исходной матрицы, а также при определении движения к оптимуму, что весьма важно при большом количестве варьируемых переменных. Кроме того, ошибка в определении целевой функции в этом методе не уводит далеко от стационарной области – потребуется лишь сделать несколько добавочных шагов. Методика по определению целевой функции состоит в следующем. 1.Составляют матрицу планирования эксперимента из условия получения ее целочисленной или почти целочисленной. Существует много методик по составлению матрицы планирования. Примем для исследований почти целочисленную матрицу. Таблица 3.5
где
2. Производят расчет координат начального симплекса по методике рассмотренной выше и определяют целевую функцию для каждого опыта; 3. Отбрасывают точки плана с наименьшим численным значением целевой функции и строят новый симплекс. Координаты новой точки симплекса х* рассчитывают из уравнения (в векторной записи)
где Для
4. Проводят эксперимент в новой точке х* и получают соответствующее значение 5.Последовательное перемещение симплекса, в процессе которого на каждом шаге происходит отбрасывание вершины симплекса с наихудшим значением целевой величины и реализация опыта в новой вершине. При этом направление перемещения центра симплекса колеблется около направления градиента. 6. Ели при перемещении симплекса на протяжении 7. Если оказывается, что целевая величина в новой вершине симплекса меньше, чем в остальных вершинах, в соответствие с логикой движения следует возвратиться к предыдущему симплексу. Чтобы предотвратить «зацикливание», в качестве отбрасываемой выбирают вершину с наименьшей (после наихудшей вершины симплекса) величиной целевой функции. 8. Если новая вершина выходит за пределы допустимой области планирования, следует поступать как в п.7. 9. При достижении области оптимума размер симплекса уменьшают (как правило, на ¼ часть начальной величины). 10. Оптимум считается достигнутым, если одна и та же точка входит в последовательные симплексы N раз, где
Выражение получено эмпирически. Другое достижение оптимума может быть получено из выражения
Где
|


 (3.9)
(3.9) - число варьируемых переменных
- число варьируемых переменных (3.10)
(3.10)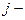 номер вершины исходного симплекса с наименьшим значением целевой функции.
номер вершины исходного симплекса с наименьшим значением целевой функции.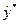 (прогнозируемое значение целевой функции в новой точке)
(прогнозируемое значение целевой функции в новой точке) (3.11)
(3.11) шагов та или иная вершина сохраняет свое положение. То симплекс совершает оборот вокруг этой вершины. Это означает что, в данной точке находится оптимум целевой функции, либо значение целевой функции в этой вершине определено не верно. Чтобы уточнить какая ситуация имеет место, в этой точке вновь проводится эксперимент и, в дальнейшем, работают с новым значением целевой величины.
шагов та или иная вершина сохраняет свое положение. То симплекс совершает оборот вокруг этой вершины. Это означает что, в данной точке находится оптимум целевой функции, либо значение целевой функции в этой вершине определено не верно. Чтобы уточнить какая ситуация имеет место, в этой точке вновь проводится эксперимент и, в дальнейшем, работают с новым значением целевой величины. (3.12)
(3.12) (13)
(13) - малая величина,
- малая величина,  среднее значение целевых величин в вершинах симплекса.
среднее значение целевых величин в вершинах симплекса.


