Гидравлический расчёт трубопроводов
Пример 3.4. Вентиляционная труба d=0,1м (100 мм) имеет длину l=100 м. Определить давление, которое должен развивать вентилятор, если расход воздуха, подаваемый по трубе, Решение. Находим скорость воздуха в трубе:
Число Рейнольдса для потока воздуха в трубе при
Относительная шероховатость (по табл. П-15
Коэффициент гидравлического трения
По формуле Дарси-Вейсбаха находим потери давления на трение (
Ответ: Пример 3.5. Расход воды при температуре 10˚ C в горизонтальной трубе кольцевого сечения, состоящей из двух концентрических оцинкованных стальных труб (при Решение. Площадь живого сечения
Смоченный периметр живого сечения
Эквивалентный диаметр
Относительная шероховатость
Средняя скорость течения
Число Рейнольдса при
Коэффициент гидравлического трения
Потери напора на трение по длине находим по формуле Дарси-Вейсбаха:
Ответ: Пример 3.6. Определить расходы воды в трубе прямоугольного поперечного сечения с отношением сторон a: b=0,25 и в круглой трубе при той же площади поперечного сечения Решение. Для трубы круглого сечения
Найдём эквивалентные диаметры для этих труб:
Потери давления определяем по формуле Дарси-Вейсбаха. Предположим первоначально, что режим течения в трубах ламинарный. Тогда по формуле Формула потерь давления принимает вид
Для круглой трубы при плотности воды
для прямоугольной трубы
Определяем числа Рейнольдса: для круглой трубы
для прямоугольной трубы
Поскольку числа Рейнольдса меньше критического равного 2320, режим течения в трубах, как и предполагалось, ламинарный. Расход воды: в круглой трубе
в прямоугольной трубе
Таким образом, в условиях ламинарного движения при одной и той же площади живого сечения и одинаковых потерях давления круглая труба пропускает расход в 2,5 раза больший, чем труба прямоугольного сечения. Ответ: Пример 3.7. Определить диаметр d нового стального трубопровода длиной l =1000м, который должен пропускать расход воды Решение. Предполагаем, что трубопровод работает в квадратичной области сопротивления, тогда найдем коэффициент Дарси по формуле Шифринсона
где Найдем среднюю скорость течения по формуле Дарси-Вейсбаха
Подставляя в это выражение формулу для λ и учитывая, что расход
получим
Для условий задачи при
d=0,15м. Площадь поперечного сечения трубы составит
Скорость в трубопроводе равна
Число Рейнольдса при
При относительной шероховатости
и числе Рейнольдса Значения λ определяем по формуле Альтшуля:
Тогда
d=0,12м. Проверка показала, что при d=0,12м и скорости 1,75м/с трубопровод работает в зоне переходного сопротивления. Уточним значение λ:
При λ=0,018
Ответ:d =0,118м. Пример 3.8. Определить расход воды в бывшей в эксплуатации водопроводной трубе диаметром d=0,3м, если скорость на оси трубы, замеренная трубкой Пито – Прандтля Решение. Находим по табл. П-15 значение абсолютной шероховатости для старых стальных труб: Предполагая, что движение воды происходит в квадратичной области турбулентного движения, определяем коэффициент гидравлического трения по формуле Шифринсона:
Среднюю скорость определяем по уравнению:
Кинематическая вязкость воды Определяем значение критерия зоны турбулентности по формуле:
Таким образом, движение действительно происходит в квадратичной области сопротивления. Расход воды в трубе находим из выражения
Ответ: Пример 3.9. Для ограничения расхода воды в водопроводной линии установлена диафрагма. Избыточные давления в трубе до и после диафрагмы постоянны и равны соответственно Решение. Потеря напора в диафрагме
Скорость воды в трубопроводе
Из формулы Вейсбаха
имеем:
Этому значению коэффициента сопротивления
где коэффициент сжатия струи находим по формуле:
Таким образом,
Находим диаметр отверстия диафрагмы:
Коэффициент сжатия струи
Ответ: Пример 3.10. Вода протекает по горизонтальной трубе, внезапно сужающейся от d1=0,2 м до d2=0,1 м. Расход воды Q=0,02 м3/с. Определить, какую разность уровней ртути hрт покажет дифференциальный манометр, включенный в месте изменения сечения. Температура воды 200С. Решение. Скорость воды в широком сечении трубы Скорость воды в узком сечении трубы Степень сужения трубопровода Коэффициент сжатия струи находим по формуле:
Коэффициент местного сопротивления при внезапном сужении определяем по формуле:
Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения, совпадающей с осью трубы,
Разность пьезометрических напоров
Величина столба ртутного манометра
Ответ: Пример 3.11. Недалеко от конца трубопроводадиаметром d=0,15 м,транспортирующего вязкую жидкость (ρ=900 кг /м3, ν=1·10-4 м2/с), имеется задвижка Лудло. Определить пьезометрическое давление перед задвижкой при расходе Q=0,04 м3/с, если степень открытия задвижки n=0,75. В конце трубопровода давление равно атмосферному. Решение. Находим скорость течения жидкости в трубе:
Число Рейнольдса, характеризующее течение в трубопроводе,
Определяем коэффициент сопротивления по формуле:
По табл. П-23 находим значение А=350, ζкв=0,2. Тогда
Потери давления найдем по формуле:
Учитывая, что в конце трубопровода избыточное давление отсутствует, пьезометрическое давление перед задвижкой будет равно 710 Па. Ответ:
Пример 3.12. Горизонтальная труба диаметром d1=0,1 м внезапно переходит в трубу диаметром d2=0,15 м. Проходящий расход воды Q=0,03 м3/с. Требуется определить: а) потери напора при внезапном расширении трубы; б) разность давлений в обеих трубах; в) потери напора и разность давлений для случая, когда вода будет течь в противоположном направлении (т.е. из широкой трубы в узкую); г) разность давлений при постепенном расширении трубы (считая потери напора пренебрежимо малыми). Решение. а) Находим потери напора при внезапном расширении трубопровода по формуле Борда:
б) Находим разность давлений в узкой и широкой трубах из уравнения Бернулли:
или
в) При изменении направления движения на обратное, т.е. из широкой трубы в узкую, скорость в сжатом сечении
Степень сжатия потока
Коэффициент сжатия трубы найдем по формуле
Разность давлений
г) Если бы был обеспечен плавный переход от трубы узкого сечения к трубе широкого сечения, то разность давлений была бы равна:
Ответ:а) Пример 3.13. Определить потери давления при движении масла в радиаторе, если расход масла Q=2·10-4 м3/с. Диаметр коллектора радиатора d0=0,03 м, диаметр трубок dтр=0,01 м, длина их lтр=1 м. Плотность масла ρ=900 кг /м3, кинематическая вязкость ν=6,5·10-5 м2/с. Решение. Скорость течения масла в коллекторах
Найдем потери давления в трубках по длине и потери на местные сопротивления. Все четыре трубки находятся в одинаковых условиях. Следовательно, расход в каждой из них
Скорость течения масла в трубке
Число Рейнольдса
Таким образом, течение в трубках ламинарное. Потери давления по длине находим по формуле Пуазейля:
Потери давления в местных сопротивлений определяем по формуле Вейсбаха:
Коэффициент местных сопротивлений вычисляем по формуле:
По табл. П-23 находим для входа в трубки: ζвх.кв=0,5 и А=30; для выхода из трубок ζвых.кв=1 и А=30. Подставляя найденные значения, получаем: ζвых=30/97+1=1,3; ζвх=30/97+0,5=0,8. Тогда
Общие потери давления при движении масла в радиаторе
Ответ: Пример 3.14. Насос забирает из водоема воду с температурой 200С в количестве Q=50 л/с. Определить максимальную высоту расположения горизонтального вала насоса над свободной поверхностью воды H1, если давление перед насосом p2=0,3·105 Па. На всасывающей чугунной трубе диаметром d=0,25 м и длиной l=50 м имеется заборная сетка, плавный поворот радиусом R=0,5 м и регулирующая задвижка, открытая на 45% площади проходного сечения. Решение. Запишем уравнение Бернулли для двух сечений 1-1 (по уровню свободной поверхности водоема) и 2-2 (перед насосом):
где V1 – средняя скорость течения воды на свободной поверхности водоема; p1 – атмосферное давление; V2 – средняя скорость течения воды во всасывающей трубе; Δpпот – сумма потерь давления по длине и местных потерь.
Учитывая, что z1=0, V1≈0, и принимая плоскость 1-1 в качестве плоскости сравнения, находим:
Высота расположения насоса над уровнем воды в водоеме
Средняя скорость течения воды во всасывающей трубе
Суммарные потери давления
где ∑ζ=ζзаб+ζпов+ζв Здесь ζзаб=5 (см. табл. П-28) – коэффициент местного сопротивления на вход во всасывающую трубу; ζпов – коэффициент местного сопротивления на плавный поворот трубопровод; ζв=5 – коэффициент местного сопротивления задвижки [9; табл. 4.21]. Число Рейнольдса (при ν=1,01·10-6 м2/с; см. табл. П-12)
Для чугунных труб kэ=1 мм [7; табл. 3.1]
По рис. 3.1 находим, что всасывающий трубопровод работает в квадратичной зоне сопротивления. Коэффициент гидравлического трения определяем по формуле Шифринсона:
Коэффициент местного сопротивления на плавный поворот ζпов вычисляем по формуле: Суммарные потери давления при плотности воды ρ=998,2 кг /м3:
Тогда
Высота расположения насоса не должна превышать 6,2 м. Ответ:
Пример 3.15. Расход горячей воды с температурой 950С через радиатор водяного отопления Q=0,1 м3/ч. Определить потери давления между сечениями 1-1 и 2-2, если диаметр подводящих трубопроводов d=0,0125 м, а общая их длина l=5 м. Решение. Суммарные потери давления
где Δpл – потери давления по длине; Δpм – местные потери.
Средняя скорость течения воды в трубопроводе
Число Рейнольдса (при ν=1,01·10-6 м2/с; см. табл. П-12)
Абсолютная шероховатость стальной трубы kэ=5·10-5 м (табл. П-15), относительная шероховатость
По рис. 3.1 находим, что трубопроводы работают в переходной зоне сопротивления. Коэффициент гидравлического трения определяем по формуле Альтшуля:
Потери давления по длине при плотности воды ρ=961,32 кг /м3 (см. табл. П-4)
Местные потери давления складываются из потерь на поворот в пробковом кране и в радиаторе. Для поворота ζ90о =1,4; для крана ζкв=0,4 (см. табл. П-23); для радиатора ζр=2 (см. табл. П-28). Эти значения коэффициентов местных сопротивлений рекомендованы для зоны квадратичного сопротивления, т.е. для больших чисел Рейнольдса. Влияние числа Рейнольдса на местные сопротивления учитываем по формуле Из табл. П-23 имеем для поворота под углом 900 A=400, для пробкового крана A=150. Для радиатора приближено принимаем A=500ζр=500·2=1000. Сумма коэффициентов местных сопротивлений
Потери давления на местные сопротивления
Суммарные потери давления
Ответ:
Решение. Запишем уравнение Бернулли для двух сечений 1-1 и 2-2, принимая уровень воды в колодце 2-2 за плоскость сравнения:
Учитывая, что p1= p2 и V1≈ V2≈0, получаем:
Потери давления в трубе
Скорость течения жидкости в трубе
Число Рейнольдса (при ν=1,01·10-6 м2/с; см. табл. П-12)
Абсолютная шероховатость чугунной трубы [7; табл. 3.1] kэ=1 мм=10-3 м. Относительная шероховатость
По рис. 3.1 находим, что труба работает в квадратичной зоне сопротивления. Коэффициент гидравлического трения вычисляем по формуле Шифринсона:
Местные потери давления складываются из потерь давления на вход в трубу и на выход из нее: ζвх=6 (табл. П-28), ζвых=1. Перепад уровней воды в водоеме и колодце
Ответ:
Решение. Разность уровней воды в водохранилище и реке определяет суммарные потери давления в сифонной трубе:
Потери давления состоят из потерь по длине и в местных сопротивлениях
Скорость движения воды в сифонном водосбросе
Примем первоначально, что водосброс работает в квадратичной области сопротивления. Тогда по формуле Шифринсона при kэ=5·10-4 м [7; табл. 3.1]
Коэффициент местного сопротивления на вход в трубу (при δ/d=0,05/1=0,05) ζвх=0,5. Коэффициент сопротивления на поворот 900 находим по формуле:
Коэффициент сопротивления на поворот 450 определяем по формуле: Сумма коэффициентов местных сопротивлений
Скорость в сифоне
Число Рейнольдса при ν=1,79·10-6 м2/с; (см. табл. П-12)
При
по рис. 3.1 устанавливаем, что водосброс работает в квадратичной области сопротивления. Расход воды через сифонный водосброс
Составим уравнение Бернулли для сечений 1-1 и 2-2:
Потери давления на участке 1-2
где l1=z2+lr=3+2=5 м и ρ=999,9 кг /м3 (см. табл. П-4). Подставляем численные значения и получаем:
Величина вакуума в верхней точке водосброса
Решение. Суммарные потери давления Δpпот складываются из потерь на трение по длине Δpл и потерь в местных сопротивлениях Δpм. Число Рейнольдса (при ν=0,55·10-6 м2/с; см. табл. П-12)
Для стального трубопровода kэ=5·10-5 (см. табл. П-15); относительная шероховатость kэ/d =5·10-5/0,0125=4·10-3. По рис. 3.1 устанавливаем, что трубопровод работает в переходной области сопротивления. Коэффициент гидравлического трения находим по формуле Альтшуля:
Потери давления на трение по длине трубопровода ρ=988,1 кг /м3 (см. табл. П-4)
Коэффициент местных сопротивлений определяем по формуле:
для поворота под углом 900 ζкв=1,4; А=400 (см. табл. П-23); для пробкового крана ζкв=0,4; А=150 (см. табл. П-23). Сумма коэффициентов местных сопротивлений
Местные потери давления
Суммарные потери давления
Если считать, что трубопровод работает в области квадратичного сопротивления, то по формуле Шифринсона найдем коэффициент Дарси
а потери давления составят:
Таким образом, потери давления, рассчитанные в предположении квадратичного закона сопротивления, будут занижены против реальных потерь на 14%. Ответ:
Решение. Потери давления при повороте на угол 90° без вставки (а) и со вставкой (б) находим по формуле:
Принимая ν=1,01·10-6 м2/с (см. табл. П-12), находим число Рейнольдса для потока воды в трубе:
Относительная шероховатость при kэ=5·10-5 м (см. табл. П-15)
Коэффициент гидравлического трения трубопровода найдем по формуле Альтшуля:
Коэффициент местного сопротивления при резком повороте на 90° (см. табл. П-20) ζ90°=1,3. Коэффициент местного сопротивления при резком повороте на 135° находим по формуле
Два поворота под углом α=135° не влияют друг на друга, если расстояние между ними больше, чем lвл. По формуле определяем длину влияния
Отсюда Таким образом, если расстояние между двумя поворотами α=135° больше, чем lвл=0,65 м, то местные сопротивления не будут оказывать влияние друг на друга. В этом случае
Вставка может снизить потери давления в 4 раза.
Пример 3.20. Из напорного бака А с отметкой горизонта воды 15,50 м требуется подать в пункт В воду на отметку 10,6 м в количестве Q = 20,6 л/сек. Между пунктами А и В расстояние l = 880 м. Для прокладки водопровода имеются «нормальные» трубы с диаметрами Решение. Определим при заданном напоре
По табл. П-16 находим Из сопоставления табличных значений K с расчетным следует, что при постановке труб Проектирование труб с Сумма потерь напора на обоих участках При При
Подставив числовые значения, воспользовавшись [4; табл. VI], получим Вес труб с Общий вес труб
|

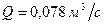 . Давление на выходе
. Давление на выходе  . Местных сопротивлений по пути не имеется. Температура воздуха 20˚ C. Труба стальная новая, бесшовная.
. Местных сопротивлений по пути не имеется. Температура воздуха 20˚ C. Труба стальная новая, бесшовная. .
.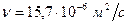 (табл. П-8)
(табл. П-8) 
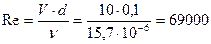 .
.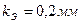 )
)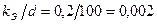 .
.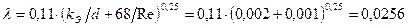 .
.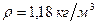 ):
):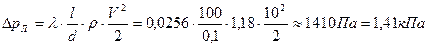 .
.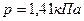 .
.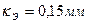 ),
), 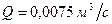 . Внутренняя труба имеет наружный диаметр d=0,075 м, а наружная труба имеет внутренний диаметр D = 0,1м. Найти потери напора на трение на длине трубы l=300м.
. Внутренняя труба имеет наружный диаметр d=0,075 м, а наружная труба имеет внутренний диаметр D = 0,1м. Найти потери напора на трение на длине трубы l=300м.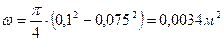 .
.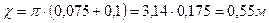 .
.
 .
.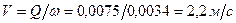 .
.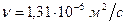 (см. табл. П-12)
(см. табл. П-12)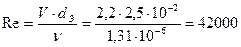 .
.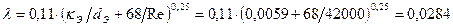 .
.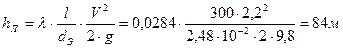 .
.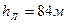 .
.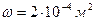 , если потери давления в этих трубах одинаковы и равны
, если потери давления в этих трубах одинаковы и равны 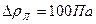 , а длина каждой трубы l=10м. Температура воды 20˚ C.
, а длина каждой трубы l=10м. Температура воды 20˚ C.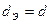 ; для трубы прямоугольного сечения при a: b =0,25
; для трубы прямоугольного сечения при a: b =0,25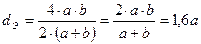 .
.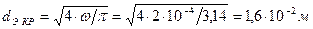 ;
;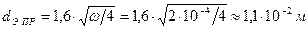 .
. , где значение коэффициента формы А (см. табл. П-24) для круглых труб равно 64, для прямоугольных – 73, найдем коэффициент Дарси.
, где значение коэффициента формы А (см. табл. П-24) для круглых труб равно 64, для прямоугольных – 73, найдем коэффициент Дарси.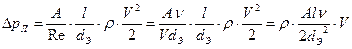 .
.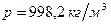 (см. табл. П-4) и вязкости
(см. табл. П-4) и вязкости 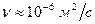 (см. табл. П-12)
(см. табл. П-12)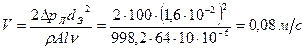 ;
;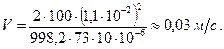
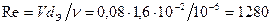 ;
;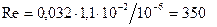 .
.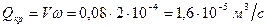 ;
;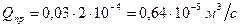 .
.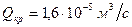 ;
; 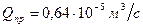 .
.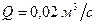 , при потерях давления
, при потерях давления 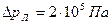 . Температура подаваемой воды 20˚ C.
. Температура подаваемой воды 20˚ C.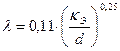 ,
,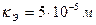 (см. табл. П-15).
(см. табл. П-15).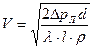 .
.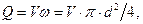
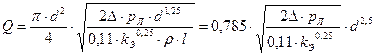 .
.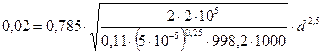 ;
;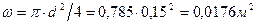 .
.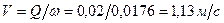 .
.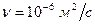 (см. табл. П-12)
(см. табл. П-12)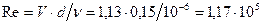 .
.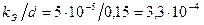
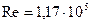 , согласно рис.3.1, находим, что трубопровод работает в зоне переходного сопротивления.
, согласно рис.3.1, находим, что трубопровод работает в зоне переходного сопротивления.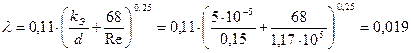 .
.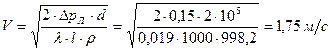 ;
;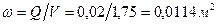 ;
;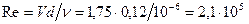 ;
;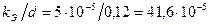 ;
;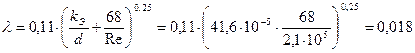 .
.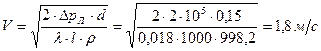 ;
;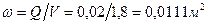 ; d =0,118м.
; d =0,118м.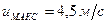 , а температура воды 10˚ C.
, а температура воды 10˚ C. .
.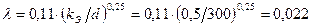 .
.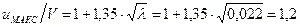 ;
;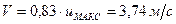 .
.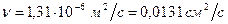 (см. табл. П-12).
(см. табл. П-12).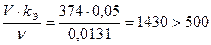 .
.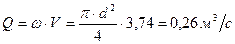 .
.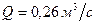 .
.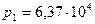 Па и
Па и 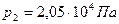 . Диаметр трубы D=0,076 м. Определить необходимый диаметр отверстия диафрагмы d с таким расчётом, чтобы расход в линии был равен
. Диаметр трубы D=0,076 м. Определить необходимый диаметр отверстия диафрагмы d с таким расчётом, чтобы расход в линии был равен 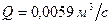 .
.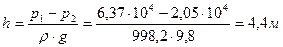 .
.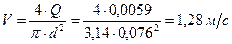 .
.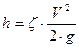
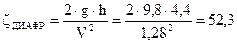 .
.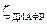 соответствует отношение площадей сечения
соответствует отношение площадей сечения 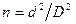 ,которое можно определить из следующей формулы:
,которое можно определить из следующей формулы: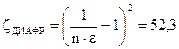 ,
,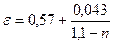 .
.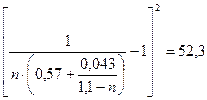 ;
;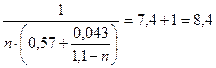 ;
;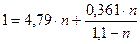 ;
;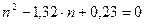 ;
;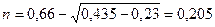 .
.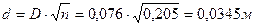 .
.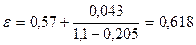 .
.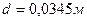 .
.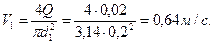
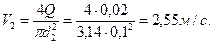
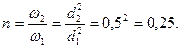
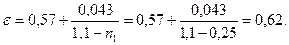
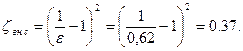
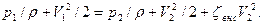
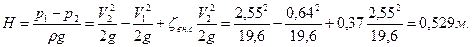
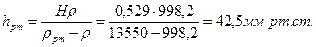
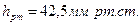
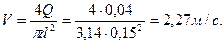
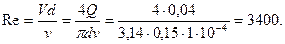
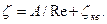
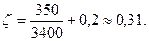

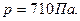
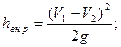
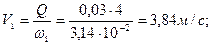
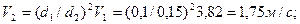
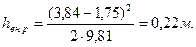
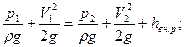
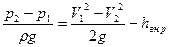
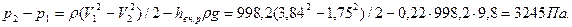
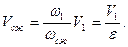
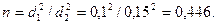
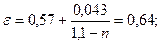
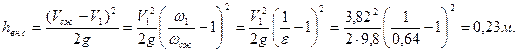
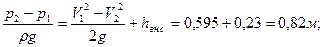
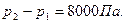
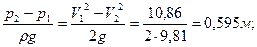
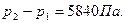
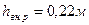 ; б)
; б) 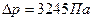 ; в)
; в) 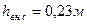 ; г)
; г)  .
.

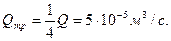
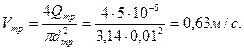
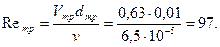
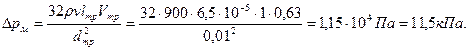
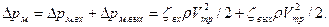
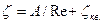

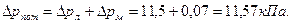

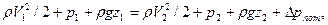
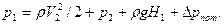

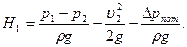
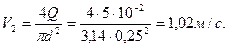

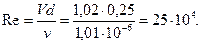
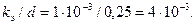
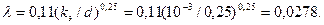
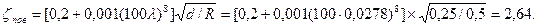
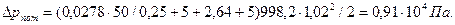
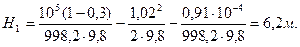



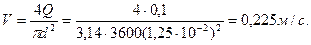
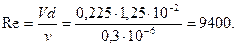
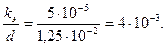
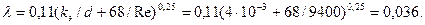

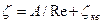
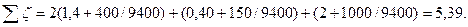



 Пример 3.16. Насос с подачей Q=0,01 м3/с забирает воду из колодца, сообщающегося с водоемом чугунной трубой диаметром d=150 мм и длиной l=100 м. На входе в трубу установлена сетка. Температура воды в водоеме 200С. Найти перепад уровней воды Δh в водоеме и колодце.
Пример 3.16. Насос с подачей Q=0,01 м3/с забирает воду из колодца, сообщающегося с водоемом чугунной трубой диаметром d=150 мм и длиной l=100 м. На входе в трубу установлена сетка. Температура воды в водоеме 200С. Найти перепад уровней воды Δh в водоеме и колодце.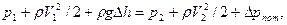
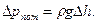
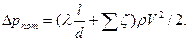
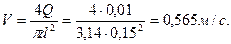
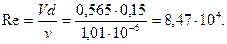
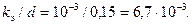

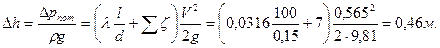
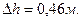
 Пример 3.17. Сифонный бетонный водосброс диаметром d=1 м, общей длиной l=50 м сбрасывает воду из водохранилища в реку, уровень которой на H=5 м ниже уровня водохранилища. Определить подачу Q сифонного водосброса, если он имеет два поворота: α=900 и α=450 с радиусами закругления R=2 м. Длина горизонтального участка lr=2 м, толщина стенок водосброса δ=0,05 м. Температура воды в водохранилище 00С. Определить также вакуум pвак в верхней точке сифона, если z1=1 м, z2=3 м.
Пример 3.17. Сифонный бетонный водосброс диаметром d=1 м, общей длиной l=50 м сбрасывает воду из водохранилища в реку, уровень которой на H=5 м ниже уровня водохранилища. Определить подачу Q сифонного водосброса, если он имеет два поворота: α=900 и α=450 с радиусами закругления R=2 м. Длина горизонтального участка lr=2 м, толщина стенок водосброса δ=0,05 м. Температура воды в водохранилище 00С. Определить также вакуум pвак в верхней точке сифона, если z1=1 м, z2=3 м.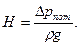
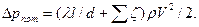

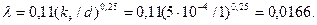
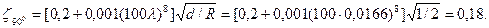
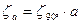 принимая а=0,7: ζ45о= ζ90 . а=0,18·0,7≈0,13. Коэффициент сопротивления на выход из трубы ζвых=1.
принимая а=0,7: ζ45о= ζ90 . а=0,18·0,7≈0,13. Коэффициент сопротивления на выход из трубы ζвых=1.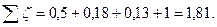
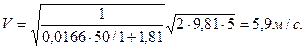
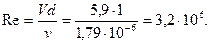
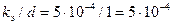
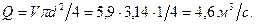
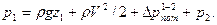
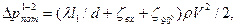

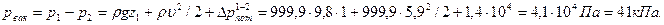 Ответ:
Ответ: 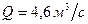 ;
; 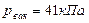 .
. Пример 3.18. В стальном трубопроводе системы горячего водоснабжения диаметром d=0,0125 м, длиной l=100 м движется вода со скоростью V=0,5 м/с. Температура воды 500С. На трубопроводе имеются два поворота под углом α=900 и пробковый кран. Определить потери давления и сравнить их с результатами расчета, выполненного в предположении квадратичного закона сопротивления.
Пример 3.18. В стальном трубопроводе системы горячего водоснабжения диаметром d=0,0125 м, длиной l=100 м движется вода со скоростью V=0,5 м/с. Температура воды 500С. На трубопроводе имеются два поворота под углом α=900 и пробковый кран. Определить потери давления и сравнить их с результатами расчета, выполненного в предположении квадратичного закона сопротивления.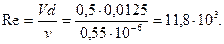
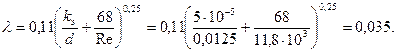
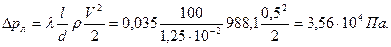
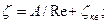
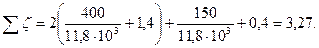
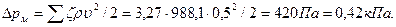
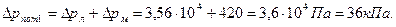
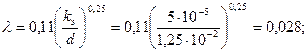
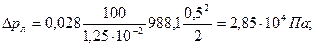
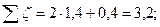
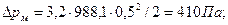
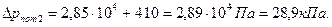
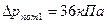 ;
; 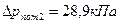 .
. Пример 3.19. Найти потери давления Δpм на преодоление местных сопротивлений при движении воды в стальном трубопроводе диаметром d=0,025 м при повороте на угол 90° без вставки и с вставкой. Найти наименьшую длину вставки lвл, при которой отсутствует взаимное влияние двух местных сопротивлений. Скорость воды V=5 м/с, температура воды 20°С.
Пример 3.19. Найти потери давления Δpм на преодоление местных сопротивлений при движении воды в стальном трубопроводе диаметром d=0,025 м при повороте на угол 90° без вставки и с вставкой. Найти наименьшую длину вставки lвл, при которой отсутствует взаимное влияние двух местных сопротивлений. Скорость воды V=5 м/с, температура воды 20°С.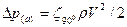 и
и 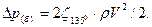
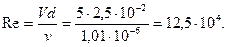
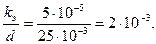
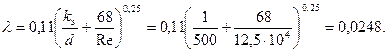
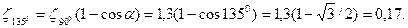
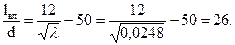
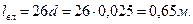
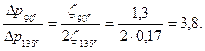
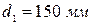 (вес 1 пог. м 38 кг, или 372,8 Н) и
(вес 1 пог. м 38 кг, или 372,8 Н) и 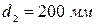 (вес 1 пог. м 55 кг, или 539,6 Н). Какие трубы надо поставить, чтобы их общий вес был наименьшим?
(вес 1 пог. м 55 кг, или 539,6 Н). Какие трубы надо поставить, чтобы их общий вес был наименьшим? расходную характеристику
расходную характеристику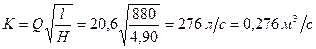 .
.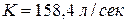 для
для 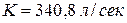 для
для  не обеспечится пропуск заданного расхода при расчетных отметках, а при
не обеспечится пропуск заданного расхода при расчетных отметках, а при 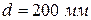 пойдет расход больше расчетного или останется излишний напор.
пойдет расход больше расчетного или останется излишний напор.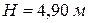 .
.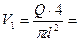
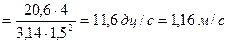 . Область сопротивления квадратичная, так как скорость
. Область сопротивления квадратичная, так как скорость 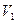 больше V, указанной в [4; табл. VI] для нормальных труб
больше V, указанной в [4; табл. VI] для нормальных труб 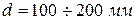 .
.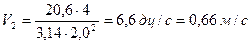 . Область сопротивления переходная, так как скорость
. Область сопротивления переходная, так как скорость 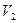 меньше указанной в [4; табл. VII] для труб
меньше указанной в [4; табл. VII] для труб 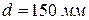 , будем иметь сумму потерь напора во всей длине трубопровода:
, будем иметь сумму потерь напора во всей длине трубопровода: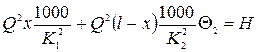 .
.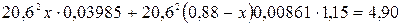 и найдем отсюда
и найдем отсюда 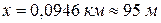 .
.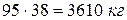 , или
, или 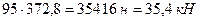 . На остальной длине
. На остальной длине 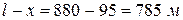 вес будет
вес будет  , или
, или 
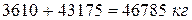 , или
, или 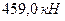 . Это будет наименьший вес при условии использования заданного напора.
. Это будет наименьший вес при условии использования заданного напора.


