Гидравлический расчёт трубопроводов. Уравнение Бернулли в этом случае имеет вид:
Уравнение Бернулли в этом случае имеет вид: Потери напора 1) потери напора, распределенные по длине потока (линейные)
2) местные потери напора
В некоторых случаях для определения потерь напора используют также формулу Шези:
а потери давления на трение по длине находят по формуле:
где При ламинарном режиме движения коэффициент гидравлического трения
а потери по длине могут быть найдены по формуле Пуазейля:
Для области гидравлически гладких труб, когда число Рейнольдса удовлетворяет условию
для определения коэффициента
Если число Рейнольдса находится в интервале:
то труба работает в переходной области сопротивления. Для указанной области коэффициент Дарси можно вычислить по формуле Альтшуля:
Если число Рейнольдса удовлетворяет условию
то в этом случае область сопротивления будет квадратичной и коэффициент гидравлического трения
а для новых стальных и чугунных водопроводных труб
Границы областей применения формулы для определения коэффициента гидравлического трения
   

Рис. 3.1. Зоны гидравлического сопротивления. Местные сопротивления вызывают изменение величины или направления скорости движения жидкости на отдельных участках трубопровода, что связано с появлением дополнительных потерь напора. В случае внезапного расширения трубопровода, местные потери напора определяются по формуле:
При внезапном сужении трубопровода потери можно определить так:
где
где В случае входа в трубу из резервуара коэффициент местного сопротивления следует принимать: - при острых входных кромках – - при закругленных кромках – - при весьма плавном входе – При выходе жидкости из трубы в резервуар, в реку и так далее коэффициент местного сопротивления принимают равным Так как коэффициент местного сопротивления при малых числах Рейнольдса зависит от последнего, то необходимо учитывать это по формуле:
где
Основные данные для расчёта местных сопротивлений представлены в приложении, табл. П-28. При гидравлическом расчёте напорных трубопроводов необходимо различать “короткие” и “длинные” трубопроводы и в случае “длинного” трубопровода потери в местных сопротивлениях можно не учитывать. Основное уравнение равномерного движения имеет вид:
где Для определения коэффициента Шези, в частности, можно использовать формулу Манинга:
При пропуске постоянного расхода по трубопроводу постоянного поперечного сечения используется формула:
где При последовательном соединении труб напор При параллельном соединении труб расход складывается из сумм расходов на отдельных линиях:
|

 .
. зависят от режима движения жидкости (ламинарный и турбулентный) и делятся на две группы:
зависят от режима движения жидкости (ламинарный и турбулентный) и делятся на две группы: , – потери, затрачиваемые на преодоление сопротивления трения, которые определяются по формуле Дарси-Вейсбаха:
, – потери, затрачиваемые на преодоление сопротивления трения, которые определяются по формуле Дарси-Вейсбаха: ;
; – потери, вызываемые резким изменением конфигурации границ потока и определяемые по формуле Вейсбаха:
– потери, вызываемые резким изменением конфигурации границ потока и определяемые по формуле Вейсбаха: .
. ,
, ,
, – эквивалентный диаметр трубопровода.
– эквивалентный диаметр трубопровода. является функцией только числа Рейнольдса и определяется по формуле:
является функцией только числа Рейнольдса и определяется по формуле: ,
, .
.
 .
. ,
, .
.
 ,
, .
.



 .
. ,
, – коэффициент сжатия струи определяется либо по таблицам, либо по формуле Альтшуля:
– коэффициент сжатия струи определяется либо по таблицам, либо по формуле Альтшуля: ,
, – степень сжатия потока.
– степень сжатия потока. ;
; ;
; .
. = 1,0, причем это значение отнесено к средней скорости в сечении перед сопротивлением.
= 1,0, причем это значение отнесено к средней скорости в сечении перед сопротивлением. ,
, – поправочный коэффициент, зависящий от местного сопротивления (табл. П-23);
– поправочный коэффициент, зависящий от местного сопротивления (табл. П-23); – табличное значение коэффициента местного сопротивления для квадратичной зоны.
– табличное значение коэффициента местного сопротивления для квадратичной зоны. ,
, – коэффициент Шези.
– коэффициент Шези. .
. ,
,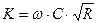 – расходная характеристика.
– расходная характеристика. складывается из суммы потерь напора на отдельных участках:
складывается из суммы потерь напора на отдельных участках: .
. .
.


