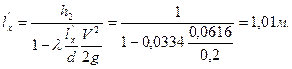Ответ: .
Пример 3.21. От напорного бака А в пункт В проложены два параллельных трубопровода. В одном из трубопроводов расход распределяется в виде непрерывной раздачи Определить: 1) Транзитный расход 2) Отметку горизонта воды в напорном баке А, обеспечивающую увеличение расхода Решение. 1) Расход в первом трубопроводе (без раздачи) определится по формуле:
где
Определим расход
Отсюда
Подставляя числовые значения, получим:
Решая уравнение, находим Следовательно, полный расход в пункте В будет:
2) Расход в пункте В увеличен вдвое, т. е.
Определим, при каком напоре будет обеспечен этот расход. Потери напора в обоих (параллельных) трубопроводах одинаковы. Следовательно, можно написать равенство, полагая расход в первом трубопроводе
или
Подставляя численные значения, получим:
Решая уравнение, найдем
Потери напора при этом
Отметка горизонта воды в бака А должна быть:
При расчете скоростными напорами в водоемах пренебречь. Наибольшее превышение над уровнем воды в водоеме принять s=2м, а глубины погружения Решение. Составим уравнение Бернулли для сечений Ι-Ι, ΙΙ-ΙΙ, расположенных на свободной поверхности, приняв за плоскость сравнения сечение ΙΙ-ΙΙ (плоскость 0-0)
откуда Подставляем последовательно местные потери и потери по длине в уравнение:
Коэффициент потерь сетки с обратным клапаном принимаем Для определения коэффициента потерь по длине λ необходимо знать режим движения. Так как в задаче требуется определить расход, то скорость неизвестна. Предполагаем, что движение происходит в квадратной зоне, и находим коэффициент С по одной из формул, например по формуле Агроскина, приняв для нормальных труб k=4,04,
где Тогда найдем коэффициент Дарси из формулы
По табл. П-28 при
и, следовательно, в формуле Вейсбаха примем
Найдем скорость в сифоне
Проверим режим движения, принимая кинематический коэффициент вязкости для воды
Определяем нижнюю границу квадратичной области по формуле
Так как в рассматриваемом случае Расход определяем по формуле
где Определим теперь, будет ли в сечении 1-1 манометрическое давление или вакуум. Составим уравнение Бернулли для сечения Ι-Ι, расположенного на свободной поверхности водоема и для произвольно выбранного сечения х - х, взятого внутри трубы. За плоскость сравнения выбираем сечение 1-1. Тогда уравнение Бернулли запишем в виде:
где
Из уравнения Бернулли найдем
Из анализа этого уравнения видно, что в сечениях, расположенных между 1-1 и 2-2, давление в сифоне будет манометрическим до тех пор, пока
Наконец, если Расположив сечение
В этом уравнении
Следовательно, в сечении 1-1 давление будет манометрическое:
где В этом уравнении неизвестным является лишь расстояние
Определим давление в сечении 2-2, внутри трубы, по исходному уравнению Бернулли
или
т. е. в сечении 2-2 будет вакуум, величина которого равна
Найдем давление в сечении 3-3, считая
Таким образом, в сечении 3-3 будет вакуум
Найдем вакуум в сечении 4-4, считая (
т.е. в сечении 4-4 также будет вакуум
Сопоставляя вакуум в сечениях 2-2 и 4-4, замечаем что вакуум в последнем сечении значительно превосходит вакуум в сечении 2-2, что объясняется увеличением потерь в сифоне по направлению течения жидкости. Уменьшение вакуума в сечении 4-4 по сравнению с сечением 3-3 объясняется уменьшением высоты zx над плоскостью сравнения. Определим давление в сечении 5-5. Чтобы упростить вычисления, составим уравнение Бернулли для произвольного сечения x`-x` и сечения II-II, приняв за плоскость сравнения 0-0. Тогда
Принимая ζвых=1, после сокращения получим:
и
Так как в сечении 5-5 геометрическая высота
т.е. Следовательно, член Сечение, в котором давление в правой вертикальной части сифона будет равно атмосферному, найдем из условия
В сечении 3-3 вакуум будет наибольшим потому, что в этом сечении при наибольшей геометрической высоте zx потери будут наибольшими. В сечениях, расположенных по течению ниже сечения 3-3, вакуум будет меньше, так как геометрическая высота уменьшается быстрее, чем нарастают потери по длине.
|

 . В пункт В поступает транзитный расход
. В пункт В поступает транзитный расход 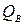 на отметку
на отметку 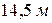 . Горизонт воды в напорном баке А расположен на отметке
. Горизонт воды в напорном баке А расположен на отметке 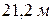 . Трубы нормальные.
. Трубы нормальные.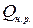 и отметка пьезометрической линии в пункте В остаются без изменения).
и отметка пьезометрической линии в пункте В остаются без изменения).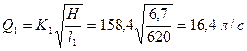 ,
, [4; табл. V] для диаметра d=150мм.
[4; табл. V] для диаметра d=150мм. Этот расход целиком поступает в водоразборный пункт В. Однако полный расход
Этот расход целиком поступает в водоразборный пункт В. Однако полный расход 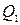 , так как во втором трубопроводе, кроме непрерывной раздачи
, так как во втором трубопроводе, кроме непрерывной раздачи  , возможно наличие транзитного расхода
, возможно наличие транзитного расхода 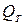 .
.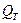 во втором трубопроводе из формулы
во втором трубопроводе из формулы .
.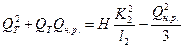 .
.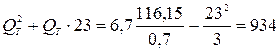 .
.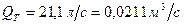 .
.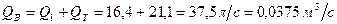 .
. .
. ,
, ,
,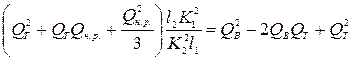 .
.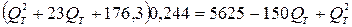 .
. . Следовательно, расход в первом трубопроводе
. Следовательно, расход в первом трубопроводе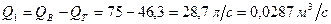 .
. .
. .
. Пример 3.22. Определить, какой расход можно перекачать сифоном из водоема А водоем В при разности горизонтов Н=1,5м, если длина сифона l=75м, а диаметр сифона d=200мм. Трубы чугунные, нормальные (Δ=1,35мм). Вычислениями выяснить, будет ли в сечениях 1-1, 2-2, 3-3, 4-4, 5-5 манометрическое давление или вакуум? Найти, где расположены сечения, в которых давление в сифоне будет равно атмосферному. Почему в сечении 3-3 будет наибольший вакуум?
Пример 3.22. Определить, какой расход можно перекачать сифоном из водоема А водоем В при разности горизонтов Н=1,5м, если длина сифона l=75м, а диаметр сифона d=200мм. Трубы чугунные, нормальные (Δ=1,35мм). Вычислениями выяснить, будет ли в сечениях 1-1, 2-2, 3-3, 4-4, 5-5 манометрическое давление или вакуум? Найти, где расположены сечения, в которых давление в сифоне будет равно атмосферному. Почему в сечении 3-3 будет наибольший вакуум?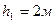 и
и 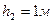 . Температура воды
. Температура воды  .
.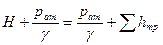
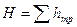 , т. е. весь напор затрачивается на преодоление сопротивлений.
, т. е. весь напор затрачивается на преодоление сопротивлений. .
.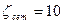 (табл. П-28).
(табл. П-28).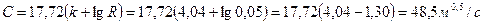 ,
,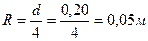 .
.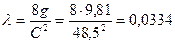 .
.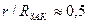 находим
находим  . Потери на выход из трубы найдем по формуле Борда-Карно
. Потери на выход из трубы найдем по формуле Борда-Карно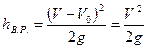 .
.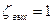 . Подставляя числовые значения в исходное уравнение, получим:
. Подставляя числовые значения в исходное уравнение, получим: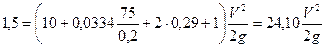 .
.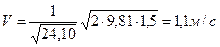 .
. при температуре
при температуре 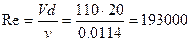 .
.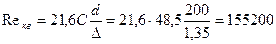 .
.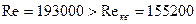 , то движение будет происходить в квадратичной области и наше предположение оказалось правильным. В противном случае нужно было бы уточнить λ и пересчитать скорость.
, то движение будет происходить в квадратичной области и наше предположение оказалось правильным. В противном случае нужно было бы уточнить λ и пересчитать скорость.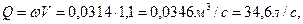
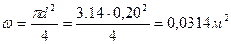 .
. ,
, - расстояние от сечения I-I до выбранного сечения;
- расстояние от сечения I-I до выбранного сечения;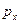 - давление в выбранном сечении;
- давление в выбранном сечении; - пьезометрическая высота, соответствующая полному давлению;
- пьезометрическая высота, соответствующая полному давлению;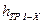 - потери напора до выбранного сечения.
- потери напора до выбранного сечения. .
.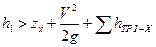 , так как в этом случае
, так как в этом случае 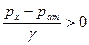 и
и 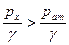 . Если
. Если 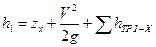 , то давление в сифоне будет равно атмосферному, так как
, то давление в сифоне будет равно атмосферному, так как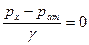 и
и 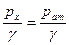 .
.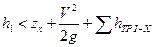 , то
, то 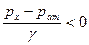 и в трубе будет вакуум
и в трубе будет вакуум  .
. в сечении 1-1, получим:
в сечении 1-1, получим: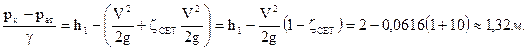
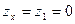 и потери до сечения 1-1 равны
и потери до сечения 1-1 равны ;
; 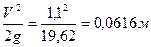
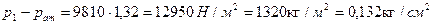 . Найдем, на каком расстоянии
. Найдем, на каком расстоянии 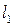 , расположено сечение
, расположено сечение 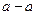 , в котором давление будет равно атмосферному. Это расстояние найдем из условия, что
, в котором давление будет равно атмосферному. Это расстояние найдем из условия, что ,
, .
.
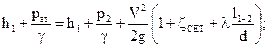
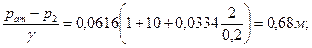
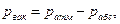

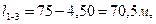

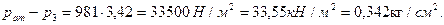
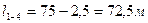 ),
),
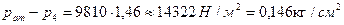 .
.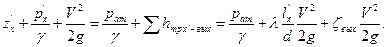

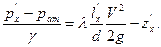
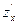 =0, то манометрическое давление найдем из уравнения
=0, то манометрическое давление найдем из уравнения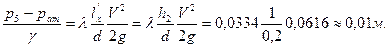
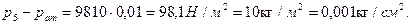
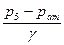 в сечении 5-5 будет превышать
в сечении 5-5 будет превышать 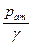 на величину напора, затрачиваемого на преодоление потерь по длине
на величину напора, затрачиваемого на преодоление потерь по длине 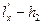 .
.