Примеры решения задач.
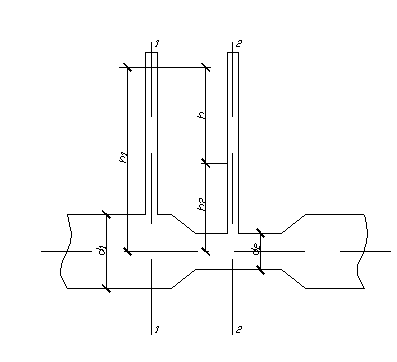
Уравнение Бернулли без учета потерь напора (энергии) Пример 3.1. Определить расход воды Q в трубе диаметром
Решение. Составим уравнение Бернулли для сечений 1-1 и 2-2, принимая за плоскость сравнения ось трубы:
Учитывая, что
Из уравнения неразрывности расхода имеем:
Поскольку
находим:
Обозначим
Тогда уравнение Бернулли запишется в виде
откуда найдем скорость в сечении 1-1:
Расход воды в трубе
где μ – коэффициент, учитывающий уменьшение расхода вследствие потерь напора; в первом приближении принимаем μ=0,98; тогда расход будет
Коэффициент μ зависит от отношения диаметров
Найдем скорость в сужении трубы
Кинематическую вязкость воды примем: С учётом полученных данных найдем число Рейнольдса
По табл. П-25 находим μ =0,98. Следовательно, в первом приближении значение μ принято верно. Искомый расход Замечание: Рассмотренное сужение трубы с плавными переходами от большего диаметра к малому и от малого к большому называется водомером Вентури. Ответ: Пример 3.2. Определить, на какую высоту поднимается вода в трубке, один конец которой присоединён к суженному сечению трубопровода, а другой конец опущен в воду. Расход воды в трубе Решение. Уравнение Бернулли для сечений 1-1 и 2-2 относительно оси трубы (потерями напора пренебрегаем) имеет вид (при
Учитывая, что скорости в сечениях 1-1 и 2-2 находятся так
то после преобразований получим:
Полученная отрицательная высота – вакуумметрическая высота. На эту высоту Ответ:
Пример 3.3. Определить критическую скорость, отвечающую переходу от ламинарного режима к турбулентному, в трубе диаметром d = 0.03 м при движении воды и воздуха при температуре 25˚C и глицерина при температуре 20˚C. Решение. Из формулы для критического числа Рейнольдса имеем:
Для воды
Для воздуха
Для глицерина
|

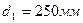 , имеющей плавное сужение до диаметра
, имеющей плавное сужение до диаметра  , если показания пьезометров: до сужения
, если показания пьезометров: до сужения  ; в сужении
; в сужении  . Температура воды
. Температура воды 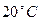 .
.
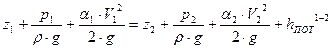 .
. , пренебрегая в первом приближении потерями напора, т. е. принимая
, пренебрегая в первом приближении потерями напора, т. е. принимая 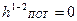 , и полагая
, и полагая  ,получим:
,получим: .
. .
. ;
; 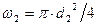 ,
, .
. .
. ,
, .
. ,
,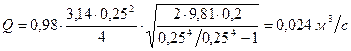 .
.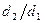 и числа Рейнольдса:
и числа Рейнольдса: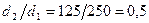 ;
;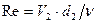 .
. .
.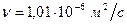 (табл. П-12).
(табл. П-12).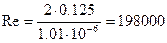 .
.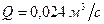 .
. , избыточное давление
, избыточное давление 
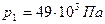 , диаметры
, диаметры 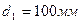 и
и  .
.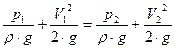 .
.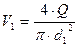 и
и  ,
,

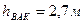 и поднимается вода в трубке.
и поднимается вода в трубке.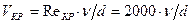 .
.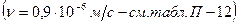
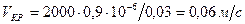 .
.
 .
.
 .
.


