Квантовое ограничение
Волна, соответствующая свободному электрону в твердом теле, может беспрепятственно распространяться в любом направлении. Ситуация кардинально меняется, когда электрон попадает в твёрдотельную структуру, размер которой L, по крайней мере в одном направлении, ограничен и по своей величине сравним с длиной электронной волны. Классическим аналогом такой структуры является струна с жёстко закрепленными концами. Колебания струны могут происходить только в режиме стоячих волн с длиной волны Аналогичные закономерности поведения характерны и для свободного электрона, находящегося в твёрдотельной структуре ограниченного размера или области твердого тела, ограниченной непроницаемыми потенциальными барьерами
Рис. 2 Возможности для движения электронов в квантовоограниченной наноразмерной структуре
На рис. 2 такая ситуация проиллюстрирована на примере квантового шнура, у которого ограничены размеры сечения a и b. В этих направлениях возможно распространение только волн с длиной, кратной геометрическим размерам структуры. Разрешенные значения волнового вектора для одного направления задаются соотношением
Запирание электрона с эффективной массой m *, по крайней мере в одном из направлений, в соответствии с принципом неопределённости приводит к увеличению его импульса на величину
Если электрон заперт в атоме, молекуле или любой потенциальной яме, то волновая функция
Рис. 3. Волновые функции и уровни энергии частицы, находящейся в бесконечно глубокой потенциальной яме. Показаны три нижних энергетических уровня (красный цвет) и три волновые функции
Стоячие волны, описывающие электронные состояния в яме, - это синусоиды, обращающиеся в точках x = 0 и x = a в нуль:
где n - номер квантового состояния, a - размер ямы. На рис. 2 изображены три такие функции, соответствующие n = 1, 2, 3,... Мы видим, что электронная плотность в яме распределяется неравномерно, есть максимумы и минимумы плотности вероятности. Из формулы (1) следует также, что длины волн
Теперь найдем разрешенные уровни энергии электрона, находящегося в потенциальной яме. Это можно сделать решив уравнение Шредингера, но мы воспользуемся сейчас правилом квантования Н. Бора. Согласно постулату Бора, в потенциальной яме разрешены лишь те траектории, для которых импульс частицы pn и ширина ямы a связаны соотношением
Здесь n - номер квантового состояния. Определив отсюда разрешенные значения импульса, без труда найдем и уровни энергии в яме:
Минимальная энергия частицы, находящейся в яме, не может быть равной нулю. Всегда существует так называемая энергия нулевых колебаний, которая, согласно формуле (3), равна Если ширина ямы равна 5 нм, то, согласно (3), имеем E1 = 0,02 эВ. Электронная масса в кристалле может существенно отличаться от массы свободного электрона m = 10-27 г. В типичной ситуации эффективная масса в квантовой яме в десять раз меньше массы свободного электрона. Тогда при той же ширине ямы получим E1 = 0,2 эВ. Эта величина и определяет характерный масштаб электронных энергий в квантовых структурах.
|

 , n = 1, 2, 3,...
, n = 1, 2, 3,...
 (n = 1, 2, 3,...), где L в соответствии с рис. 1 может принимать значения, равные a или b. Для соответствующих им электронов это означает, что они могут иметь только определенные фиксированные значения энергии, то есть имеет место дополнительное квантование энергетических уровней. Это явление получило название квантового ограничения. Вдоль же шнура могут двигаться электроны с любой энергией.
(n = 1, 2, 3,...), где L в соответствии с рис. 1 может принимать значения, равные a или b. Для соответствующих им электронов это означает, что они могут иметь только определенные фиксированные значения энергии, то есть имеет место дополнительное квантование энергетических уровней. Это явление получило название квантового ограничения. Вдоль же шнура могут двигаться электроны с любой энергией.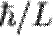 . Соответственно увеличивается и кинетическая энергия электрона на величину
. Соответственно увеличивается и кинетическая энергия электрона на величину  . Таким образом, квантовое ограничение сопровождается как увеличением минимальной энергии запертого электрона, так и дополнительным квантованием энергетических уровней, соответствующих его возбужденному состоянию. Это приводит к тому, что электронные свойства наноразмерных структур отличаются от известных объёмных свойств материала, из которого они сделаны.
. Таким образом, квантовое ограничение сопровождается как увеличением минимальной энергии запертого электрона, так и дополнительным квантованием энергетических уровней, соответствующих его возбужденному состоянию. Это приводит к тому, что электронные свойства наноразмерных структур отличаются от известных объёмных свойств материала, из которого они сделаны. представляет стоячую волну. Если речь идет о прямоугольной потенциальной яме, которая изображена на рис. 3, то по своей форме волна будет такой же, как и в случае натянутой струны, однако, во-первых, природа волны здесь иная, а во-вторых, дискретным в этом случае будет не спектр частот, а спектр энергий.
представляет стоячую волну. Если речь идет о прямоугольной потенциальной яме, которая изображена на рис. 3, то по своей форме волна будет такой же, как и в случае натянутой струны, однако, во-первых, природа волны здесь иная, а во-вторых, дискретным в этом случае будет не спектр частот, а спектр энергий.
 , (1)
, (1) -функций, описывающих электронные состояния с различными n, удовлетворяют условиям
-функций, описывающих электронные состояния с различными n, удовлетворяют условиям 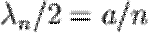 , то есть в яме укладывается целое число полуволн.
, то есть в яме укладывается целое число полуволн.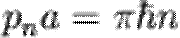 (2)
(2)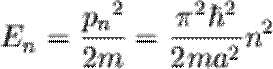 (3)
(3) .
.


