ОБЩАЯ ЧАСТЬ. Задане електричне коло має три вітки, два вузла і два лінійно незалежних контури
Задане електричне коло має три вітки, два вузла і два лінійно незалежних контури. Задаємо умовні додатні напрями струмів у вітках.
Вибравши напрями обходу контурів за напрямом обертання годинникової стрілки, складаємо рівняння за другим законом Кірхгофа для напруг на елементах контурів
Об’єднуємо рівняння, складені за першим і другим законами Кірхгофа, в систему
Враховуючи залежності між струмами і напругами ідеальних елементів (5.6), (5.7), (5.8) систему рівнянь представимо у вигляді
Отримана система містить інтегро-диференціальні рівняння. Щоб перейти до диференціальних рівнянь, виразимо струм ємнісного елемента через напругу
і підставимо цей вираз в систему (5.101)
У результаті підстановки (5.103) отримано систему звичайних диференціальних рівнянь (5.104) з постійними коефіцієнтами відносно невідомих струмів у вітках iL (t), iR (t) і напруги на ємнісному елементі uC (t).
Визначення вимушених складових струмів і напруг. Вимушені складові струмів і напруг обумовлені дією джерел електричної енергії і тому наявні в електричному колі як в усталеному, так і перехідному режимах. Як вже зазначалося, вимушені складові відповідають частинному розв’язку системи диференціальних рівнянь. Оскільки у досліджуваному колі (рис. 5.9) в усталеному режимі після закінчення перехідного процесу діє джерело постійної напруги зі значенням 2 U 0, то опір індуктивного елемента вважається нескінченно малим, а опір ємнісного елемента — нескінченно великим. Схема заміщення електричного кола у цьому режимі наведена на рис. 5.10. Користуючись цією схемою заміщення, легко розрахувати вимушені складові струмів у вітках і напругу на ємності. Визначення вільних складових струмів і напруг. Вільні складові струмів і напруг, як вже зазначалося раніше, обумовлені енергією, накопиченою реактивними елементами кола. Щоб визначити вільні складові струмів чи напруг, потрібно розв’язати систему однорідних диференціальних рівнянь, складених за законами Кірхгофа. Наприклад, однорідні диференціальні рівняння для кола, зображеного на рис.5.9 матимуть вигляд:
Розв’язком однорідного диференціального рівняння є лінійна комбінація експоненціальних функцій. Для досліджуваного кола загальний розв’язок системи диференціальних рівнянь матиме вигляд
Виведення характеристичного рівняння та знаходження його коренів. Щоб знайти корені р 1, р 2,..., рn характеристичного рівняння підставляємо у систему однорідних диференціальних рівнянь (5.106) загальний розв’язок у формі експоненціальних функцій. Далі виконуємо операції диференціювання, які для експоненціальної функції рівносильні множенню цієї функції на показник степеня. У результаті виконання цих операцій отримуємо систему алгебраїчних рівнянь
Таким чином, використовуючи властивості диференціювання і інтегрування експоненціальних функцій (5.10) і (5.11), можна звести систему однорідних диференціальних рівнянь до системи алгебраїчних рівнянь. Така процедура називається алгебраїзацією системи однорідних диференціальних рівнянь. Визначник D цієї системи алгебраїчних рівнянь дорівнюватиме
Як випливає з попереднього аналізу, умовою існування ненульового розв’язку системи алгебраїчних рівнянь (5.108) є умова:
Рівняння (5.110) є характеристичним рівнянням системи алгебраїчних рівнянь (5.108). Невідомим у цьому рівнянні є параметр р. Для заданого електричного кола характеристичне рівняння має вигляд
Це рівняння другої степені, тобто квадратне рівняння і має два корені. Відповідне зведене квадратне рівняння має вигляд
Якщо ввести позначення
то зведене характеристичне рівняння (5.112) матиме вигляд
Корені цього квадратного рівняння визначаються за формулою
Величини t 1, t 2 мають розмірність часу і тому називаються сталими часу. Від сталих часу залежить тривалість перехідного процесу. Величина w 0 має розмірність кутової частоти і тому називається власною частотою вільних коливань системи. Вільні складові, обумовлені енергією, накопиченою реактивними елементами, з часом згасають. Ступінь згасання характеризується величиною d, яка називається коефіцієнтом згасання і має розмірність обернену розмірності часу. Сталі часу і корені характеристичного рівняння для заданого електричного кола мають такі значення
Корені характеристичного рівняння можна визначити і іншим способом. Спочатку визначається комплексний вхідний опір Zx(j w ) заданого електричного кола на синусоїдному струмі відносно будь-якої розімкненої вітки. Далі замінюємо аргумент j w на аргумент р і прирівнюємо його до нуля
Отримане рівняння (5.36) є характеристичним рівнянням заданого електричного кола. Наприклад, для заданого електричного кола (рис. 5.) вхідний опір на синусоїдному струмі дорівнюватиме
Замінивши jw на р і прирівнявши вираз до нуля
отримаємо характеристичне рівняння другого степеня
Порівнявши вирази (5.111) і (5.120), бачимо, що характеристичні рівняння, отримані різними методами однакові. Визначення сталих інтегрування. Як вже зазначалося, загальний розв’язок однорідного диференціального рівняння, що відповідає вільним складовим струмів і напруг, знаходиться як сума експоненціальних функцій
де i'L(t), i'R(t),uC'(t) — відповідно, вільні складові струмів у вітках і напруги на ємнісному елементі кола; С 11, С 12,..., Сnm — сталі інтегрування; p1, p2 — корені характеристичного рівняння. Таким чином, щоб визначити вільні складові струмів і напруг, потрібно знайти корені характеристичного рівняння і значення сталих інтегрування. Раніше було показано, як знаходяться корені характеристичного рівняння. Розглянемо тепер, як знаходяться значення сталих інтегрування. Щоб розв’язати диференціальне рівняння, що описує реальних фізичний об’єкт, наприклад електричне коло, потрібно знати так звані початкові умови. Для електричних кіл початковими умовами є перехідні струми в індуктивних елементах і напруги на ємнісних елементах в момент часу безпосередньо після комутації (t=0+), тобто
За законами комутації, значення струмів в індуктивних елементах і напруг на ємнісних елементах у момент комутації не змінюються
Обчислимо значення струму в індуктивному елементі iL(0_) і напруги на ємнісному елементі uC(0_) в усталеному режимі до моменту комутації. У цьому усталеному режимі на вході кола діє джерело постійної напруги зі значенням U 0. Схема заміщення досліджуваного електричного кола в усталеному режимі до моменту комутації наведена на рис. 5.3, де враховано, що опір індуктивного елемента є нескінченно малий, а опір ємнісного елемента — нескінченно великий.
За законом Ома знаходимо струм в індуктивному елементі і напругу на ємнісному елементі до моменту комутації Підставляємо ці значення у праву частину системи рівнянь (5.42)
Таким чином, на основі законів комутації отримано систему з двох рівнянь відносно чотирьох невідомих С 11, С 12, С 31, С 32. Щоб обчислити значення сталих інтегрування, складаємо ще два рівняння за законами Кірхгофа і визначимо струм у ємнісному елементі iC (0+) і напругу на індуктивному елементі uL (0+) у момент часу безпосередньо після комутації, враховуючи той факт, що напруга на ємнісному елементі uС (0+) і струм в індуктивному елементі iL (0+) знайдені за законами комутації і значення їх відомі
Зведемо систему до двох рівнянь
Значення i ׳ L(0+) і u ׳ C(0+) знайдемо із системи рівнянь (5.42)
і підставимо ці вирази у систему (5.48)
Розв’язавши систему рівнянь, отримуємо значення
Оскільки вільні складові струму в індуктивному елементі і напруги на ємнісному елементі записуються у формі
То їх похідні у момент t =0+ дорівнюватимуть
Об’єднуємо систему рівнянь (5.46) і (5.53) у єдину систему рівнянь
Розв’язавши отриману систему рівнянь, отримуємо значення для сталих інтегрування значення
Сталі інтегрування C 11, C 12 та C 31, C 32 є комплексно сполученими величинами, тобто для них справедливі такі співвідношення.
Корені p 1, p 2, згідно з (5.116), також є комплексно сполученими
Враховуючи співвідношення (5.137), (5.138), а також взявши до уваги відомі формули
вирази (5.136) для струму і напруги можна записати так:
де
Графіки струму у індуктивному елементі і напруги на ємнісному елементі наведені на рис. 5.12.
ОБЩАЯ ЧАСТЬ
|

 Для одного з двох вузлів складаємо за першим законом Кірхгофа рівняння
Для одного з двох вузлів складаємо за першим законом Кірхгофа рівняння . (5.99)
. (5.99) . (5.100)
. (5.100) . (5.101)
. (5.101) . (5.102)
. (5.102) , (5.103)
, (5.103) . (5.104)
. (5.104) Рис. 5.10
Рис. 5.10

 . (5.106)
. (5.106) (5.107)
(5.107) . (5.108)
. (5.108) . (5.109)
. (5.109) . (5.110)
. (5.110) (5.111)
(5.111) . (5.112)
. (5.112) , (5.113)
, (5.113) . (5.114)
. (5.114) . (5.115)
. (5.115)




 . (5.117)
. (5.117) . (5.118)
. (5.118) , (5.119)
, (5.119) . (5.120)
. (5.120) , (5.121)
, (5.121) .(5.122)
.(5.122) . (5.123)
. (5.123) Рис. 5.11
Рис. 5.11
 (5.124)
(5.124)
 (5.125)
(5.125)
 . (5.126)
. (5.126) . (5.127)
. (5.127) . (5.128)
. (5.128) , (5.129)
, (5.129) . (5.130)
. (5.130) . (5.131)
. (5.131) , (5.132)
, (5.132) .(5.133)
.(5.133) . (5.134)
. (5.134)



 Обчислені значення коренів p 1, p 2 і сталих інтегрування C 11, C 12, C 31, C 32 підставляємо у вираз для струму в індуктивному елементі і напруги на ємнісному елементі значення.
Обчислені значення коренів p 1, p 2 і сталих інтегрування C 11, C 12, C 31, C 32 підставляємо у вираз для струму в індуктивному елементі і напруги на ємнісному елементі значення.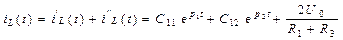









 ,
,


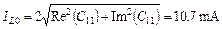 ;
; ;
; ;
; ;
; ;
; .
.


