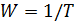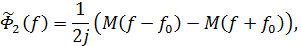Будем считать что 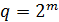 , где m – целое; число m может рассматриваться как число бит переносимых сигналом (при отсутствии кодирования). Поставим в соответствие номеру сигнала i, i=0,1,…q-1, пару целых i1 и i2,
, где m – целое; число m может рассматриваться как число бит переносимых сигналом (при отсутствии кодирования). Поставим в соответствие номеру сигнала i, i=0,1,…q-1, пару целых i1 и i2,  , по правилу
, по правилу 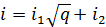 . Иначе говоря,
. Иначе говоря,  это цифры в
это цифры в 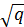 -ичном представлении числа i. Положим, что
-ичном представлении числа i. Положим, что
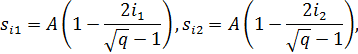

где A- максимальное абсолютное значение величин si1 и si2. Очевидно, что значение величин si1 и si2 расположены с равномерным шагом в интервале [-A,A]. Сигнальное множество КАМ показано на рисунке ниже.
q=4 q=16 q=64
Минимальное расстояние между сигналами
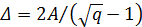
Энергия i-го сигнала равна

Средняя энергия сигналов


Решающие области для сигнальных точек, находящихся в середине сигнального созвездия, представляют собой квадраты. Для точек на краях сигнального созвездия они бесконечны
Расчет недостающих параметров
Количество бит переносимых одним сигналом m
 бит
бит
Количество сигналов q
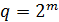 =4 сигнала
=4 сигнала
Период следования сигналов T
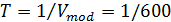 с
с
Выбор базиса и огибающей
В качестве огибающей выберем функцию

Вид этой функции показан на рисунке расположенном ниже.
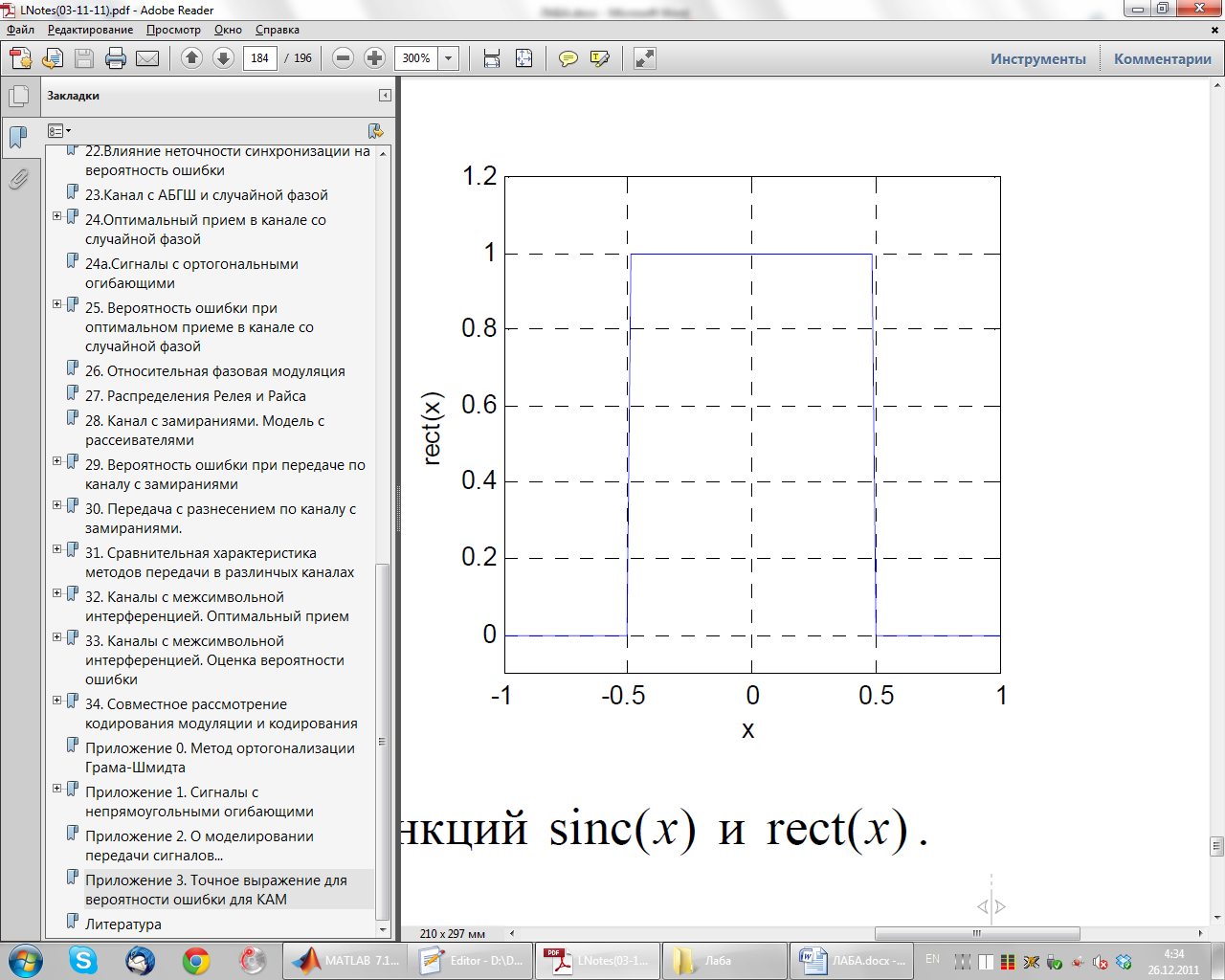
Ширина полосы частот занимаемых сигналами равна 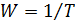
Базисы на основе этой огибающей 
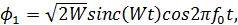

где  .
.
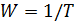
Вычисление спектров сигналов
Для базисов  преобразование Фурье имеет вид:
преобразование Фурье имеет вид:

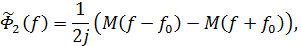
где функция M определена как:


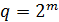 , где m – целое; число m может рассматриваться как число бит переносимых сигналом (при отсутствии кодирования). Поставим в соответствие номеру сигнала i, i=0,1,…q-1, пару целых i1 и i2,
, где m – целое; число m может рассматриваться как число бит переносимых сигналом (при отсутствии кодирования). Поставим в соответствие номеру сигнала i, i=0,1,…q-1, пару целых i1 и i2,  , по правилу
, по правилу 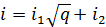 . Иначе говоря,
. Иначе говоря,  это цифры в
это цифры в 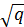 -ичном представлении числа i. Положим, что
-ичном представлении числа i. Положим, что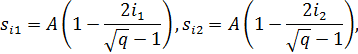
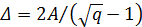


 бит
бит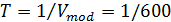 с
с

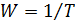

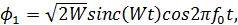

 .
.