Лабораторная работа №1. Цель: Изучение основного закона динамики вращательного движения, определение момента инерции тела.
Цель: Изучение основного закона динамики вращательного движения, определение момента инерции тела. Приборы и принадлежности: Маятник Обербека, весы, штангенциркуль, рулетка, секундомер
Общие положения В работе экспериментально проверяется основное уравнение динамики вращательного движения вокруг неподвижной оси. При изучении динамики вращательного движения пользуются понятием момента инерции тела. Момент инерции J относительно оси вращения называется физическая величина равная сумме произведений n масс на квадрат расстояний до оси вращения:
В случае непрерывного распределения масс эта сумма сводится к интегралу
Если известен момент инерции тела относительно центра масс, то момент инерции относительно другой параллельной оси вращения определяется теоремой Штейнера..
где: J - момент инерции тела относительно произвольной оси вращения, J 0 - момент инерции тела относительно центра масс, d - расстояние между осью проходящей через центр масс и осью вращения тела. При вращательном движении твердого тела вводится понятие момента силы. Момент силы M относительно неподвижной оси вращения называется физическая величина, определяемая произведением векторов силы F и радиуса-вектора r, проведенного из точки 0 (на оси вращения) к точке приложения силы (рис.12.1)
Модуль момента сила
где l = r· sin a - кратчайшее расстояние между линией действия силы и точкой 0 называется плечом силы. Основное уравнение динамики вращательного движения вокруг неподвижной оси
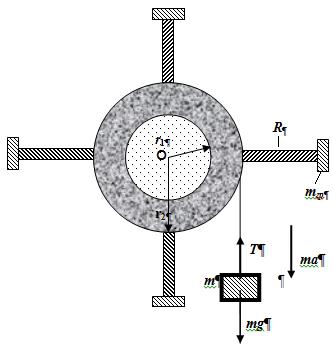
где e - угловое ускорение. Для экспериментального определения законов динамики вращательного движения используется маятник Обербека, который представлен на рис.12.2. Он представляет собой колесо в виде крестовины. На четырех взаимно перпендикулярных стержнях могут перемещаться грузы массой mгр каждый. На горизонтальной оси крестовины имеется двухступенчатый диск радиусами r 1 и r 2 , на которые наматывается нить. Один конец нити прикреплен к диску, на втором подвешен падающий груз. Под влиянием падающего груза нить разматывается с диска и вызывает вращательное ускоренное движение крестовины. Вращающий момент диска вызывает сила натяжения нити Т.
где: Т – сила натяжения нити, ri – выбранный радиус двухступенчатого диска (r 1 или r 2). Согласно второму закону Ньютона можно записать уравнение движения падающего груза
где: m – масса падающего груза, а – ускорение. Ускорение а связано с угловым ускорением соотношением
С учетом вышесказанного получим значение момента силы
Согласно уравнению кинематики поступательного движения для падающего груза
где: h – высота падения груза, Из уравнения (12.10) определяется ускорение а.
Учитывая формулы (12.8-12.10) получим выражение для момента инерции
Момент инерции входящий в формулу (12.13) определяется согласно теореме Гюйгенса-Штейнера и записывается в виде
где R – расстояние от груза до оси вращения, J 0 - -момент инерции маятника относительно центра масс. Принцип работы маятника На спицах крестовины маятника Обербека укрепляются 4 груза, имеющих равные массы mгр. Изменяя положение грузов mгр , меняем момент инерции маятника. На шкив намотана нить, один конец которой закреплен на шкиве, а к другому прикреплен груз массой т. Если маятник Обербека предоставить самому себе, то концы нити будут действовать как на шкив, так и на груз с одинаковой по величине силой, равной силе натяжения нити Т. Сила Т создает вращающий момент, поэтому шкив будет вращаться, а груз т опускаться до тех пор, пока нить не размотается полностью. После этого за счет запаса кинетической энергии нить будет вращаться, а груз т - опускаться до тех пор, пока нить не размотается полностью. После этого за счет запаса кинетической энергии шкив будет продолжать вращаться в ту же сторону, наматывая на себя нить и подымая груз до тех пор, пока весь запас кинетической энергии не будет превращен в потенциальную поднятого груза и работу по преодолению сил трения. Затем процессы опускания и поднятия грузов будут повторяться. Эта повторяемость процессов дала основание назвать рассматриваемое устройство мятником. Ход работы 1. Измерить штангенциркулем диаметр шкива и определить его радиус. 2.Закрепить грузы mгр на спицах так, чтобы маятник находился в равновесии. 3.Измерить расстояние R от оси вращения до центра подвижного груза, массой mгр . 4. Измерить h - высоту падения груза. 5. Определить масcу m груза, который падает. Намотать нить на шкив и установить груз т в начальном положении. 6. Освободить груз т, одновременно пустив в ход секундомер. Измерить время t падения груза. Опыт повторить 5 раз. Найти среднее время падения t ср. 7.Изменить на 2÷ 3 см расстояние R и повторить пп.2-6. 8.Радиус R менять не менее 5 раз. Данные занести в табл. 12.1. 9.Рассчитать момент инерции используя формулу (12.13), вычисления занести в табл. 12.1 10. Построить график зависимости J = f (R 2 ) и убедиться что J = f (R 2 ) является линейной функцией. Прямую экстраполировать до пересечения с ось ординат, как показано на рис. 12.3. Из графика определить J 0.
10.Зная J 0 проверить соответствие формул (12.13) и (12.14).
Таблица 12.1.
11. Посчитать абсолютную и относительную погрешности для J 0 и J. 12. Записать истинное значение измеренной величины
Контрольные вопросы: 1. Как определить момент инерции тела. 2. Что такое момент силы относительно неподвижной оси. 3. Основное уравнение динамики вращательного движения. 4. Теорема Гюйгенса-Штейнера ее физический смысл. 5. Как графически определить J 0. 6. Связь линейных и угловых характеристик вращательного движения. 7. Вывести расчетную формулу с использованием теоремы Штейнера.
Лабораторная работа №1
|

 . (12.1)
. (12.1) . (12.2)
. (12.2) , (12.3)
, (12.3)
 . (12.4)
. (12.4) . (12.5)
. (12.5) , (12.6)
, (12.6) , (12.7)
, (12.7) , (12.8)
, (12.8)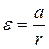 . (12.9)
. (12.9) . (12.10)
. (12.10) . (12.11)
. (12.11) . (12.12)
. (12.12)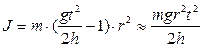 . (12.13)
. (12.13) , (12.14)
, (12.14)