нтервальное оценивание
(описание работы соответствует функциЯм Excel, в R-project используйте аналогичные функции)
1. ‘моделируйте генеральную совокупность из 200 значений нормально распределенной случайной величины. ‡апишите использованные при этом значениЯ математического ожиданиЯ  и среднеквадратического отклонениЯ
и среднеквадратического отклонениЯ  . ЏостроеннаЯ генеральнаЯ совокупность ЯвлЯетсЯ выборкой из нормального распределениЯ объема
. ЏостроеннаЯ генеральнаЯ совокупность ЯвлЯетсЯ выборкой из нормального распределениЯ объема  Џостройте гистограмму и полигон относительных частот длЯ смоделированной генеральной совокупности (длЯ 8 и 12 интервалов разбиениЯ).
Џостройте гистограмму и полигон относительных частот длЯ смоделированной генеральной совокупности (длЯ 8 и 12 интервалов разбиениЯ).
2. ‚ычислите дисперсию  и среднеквадратическое отклонение
и среднеквадратическое отклонение  полученной генеральной совокупности, с помощью функций „€‘Џђ и ‘’ЂЌ„Ћ’Љ‹ЋЌЏ соответственно. ‚ычислите математическое ожидание смоделированной генеральной совокупности
полученной генеральной совокупности, с помощью функций „€‘Џђ и ‘’ЂЌ„Ћ’Љ‹ЋЌЏ соответственно. ‚ычислите математическое ожидание смоделированной генеральной совокупности 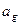 .
.
3. ‚ычислите вероЯтность попаданиЯ случайной величины  в интервал [5;11]:
в интервал [5;11]:  . „лЯ нахождениЯ значений функции распределениЯ
. „лЯ нахождениЯ значений функции распределениЯ 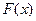 нормальной случайной величины воспользуйтесь функцией ЌЋђЊђЂ‘Џ, аргументами которой ЯвлЯютсЯ:
нормальной случайной величины воспользуйтесь функцией ЌЋђЊђЂ‘Џ, аргументами которой ЯвлЯютсЯ:
X С аргумент функции распределениЯ (граница интервала);
‘реднее С математическое ожидание случайной величины  ;
;
‘тандартное_откл С среднеквадратическое отклонение  ;
;
€нтегральный С параметр, указывающий функцию длЯ вычислениЯ (при вычислении значениЯ функции распределениЯ значение полЯ должно быть 1).
‚ычислите аналогичную вероЯтность (относительную частоту) длЯ смоделированной генеральной совокупности. ‘равните вероЯтности.
4. ‘генерируйте две случайные выборки объемом 30 значений из исходной нормально распределенной генеральной совокупности (с математическим ожиданием  и среднеквадратическим отклонением
и среднеквадратическим отклонением  ).
).
5. „лЯ каждой выборки постройте точечные оценки параметров распределениЯ (приведены названиЯ функций):
‚ыборочное среднее  (‘ђ‡ЌЂ—);
(‘ђ‡ЌЂ—);
‚ыборочнаЯ дисперсиЯ (несмещеннаЯ)  („€‘Џ);
(„€‘Џ);
‚ыборочное среднеквадратическое отклонение  (‘’ЂЌ„Ћ’Љ‹ЋЌ).
(‘’ЂЌ„Ћ’Љ‹ЋЌ).
‚ дальнейшем понадобитсЯ объем выборки. …го можно вычислить с помощью функции ‘—…’.
6. „лЯ каждой из выборок постройте гистограммы относительных частот (5 и 7 интервалов)
7. Ќайдите доверительный интервал длЯ оценки неизвестного математического ожиданиЯ с уровнем довериЯ 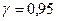 , предполагаЯ, что известно среднеквадратическое отклонение генеральной совокупности
, предполагаЯ, что известно среднеквадратическое отклонение генеральной совокупности  (здесь и далее в пп 9 и 10 доверительные интервалы строЯтсЯ по трем выборкам и в отчете располагаютсЯ рЯдом, сделайте выводы о размахе полученных доверительных интервалов)
(здесь и далее в пп 9 и 10 доверительные интервалы строЯтсЯ по трем выборкам и в отчете располагаютсЯ рЯдом, сделайте выводы о размахе полученных доверительных интервалов)
„лЯ этого вычислите значение  , входЯщее в формулу доверительного интервала с помощью функции Excel ЌЋђЊ‘’ЋЃђ (можно также воспользоватьсЯ функцией ЌЋђЊЋЃђ, указав в качестве среднего значениЯ 0, а в качестве стандартного отклонениЯ 1). „лЯ того чтобы правильно воспользоватьсЯ функцией ЌЋђЊ‘’ЋЃђ, необходимо учесть, что значение полЯ ‚ероЯтность в этой функции представлЯет собой вероЯтность
, входЯщее в формулу доверительного интервала с помощью функции Excel ЌЋђЊ‘’ЋЃђ (можно также воспользоватьсЯ функцией ЌЋђЊЋЃђ, указав в качестве среднего значениЯ 0, а в качестве стандартного отклонениЯ 1). „лЯ того чтобы правильно воспользоватьсЯ функцией ЌЋђЊ‘’ЋЃђ, необходимо учесть, что значение полЯ ‚ероЯтность в этой функции представлЯет собой вероЯтность  , т.е. равно площади под графиком плотности от
, т.е. равно площади под графиком плотности от  до
до  . Џоэтому следует взЯть значение вероЯтности равное 0,95+0,05/2=0,975. ќто значение указываетсЯ в поле ‚ероЯтность.
. Џоэтому следует взЯть значение вероЯтности равное 0,95+0,05/2=0,975. ќто значение указываетсЯ в поле ‚ероЯтность.
‚ычислите границы доверительного интервала по формуле
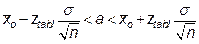 .
.
Џроверьте полученное значение точности оценки  с помощью функции „Ћ‚…ђ€’.
с помощью функции „Ћ‚…ђ€’.
8. Џостройте доверительный интервал длЯ оценки математического ожиданиЯ при неизвестном значении генерального среднеквадратического отклонениЯ по формуле

где  С среднеквадратическое отклонение, вычисленное по несмещенной выборочной дисперсии, а
С среднеквадратическое отклонение, вычисленное по несмещенной выборочной дисперсии, а  находитсЯ по заданному значению уровнЯ довериЯ 0,95 по таблице распределениЯ ‘тьюдента длЯ
находитсЯ по заданному значению уровнЯ довериЯ 0,95 по таблице распределениЯ ‘тьюдента длЯ  степеней свободы или с помощью функции ‘’њћ„ђЂ‘ЏЋЃђ.
степеней свободы или с помощью функции ‘’њћ„ђЂ‘ЏЋЃђ.
9. Ќайдите доверительный интервал с уровнем довериЯ 0,95 длЯ дисперсии при неизвестном значении генерального среднего по формуле
 ,
,
и длЯ генерального среднеквадратического отклонениЯ по формуле
 ,
,
где  С среднеквадратическое отклонение, вычисленное по несмещенной выборочной дисперсии,
С среднеквадратическое отклонение, вычисленное по несмещенной выборочной дисперсии,  находитсЯ по заданному значению уровнЯ довериЯ 0,025 по таблице распределениЯ Џирсона хи-квадрат длЯ
находитсЯ по заданному значению уровнЯ довериЯ 0,025 по таблице распределениЯ Џирсона хи-квадрат длЯ  степеней свободы или с помощью функции
степеней свободы или с помощью функции
хи2обр,  находитсЯ по заданному значению уровнЯ довериЯ 0,975 по таблице распределениЯ Џирсона хи-квадрат длЯ
находитсЯ по заданному значению уровнЯ довериЯ 0,975 по таблице распределениЯ Џирсона хи-квадрат длЯ  степеней свободы или с помощью функции
степеней свободы или с помощью функции

 и среднеквадратического отклонениЯ
и среднеквадратического отклонениЯ  . ЏостроеннаЯ генеральнаЯ совокупность ЯвлЯетсЯ выборкой из нормального распределениЯ объема
. ЏостроеннаЯ генеральнаЯ совокупность ЯвлЯетсЯ выборкой из нормального распределениЯ объема  Џостройте гистограмму и полигон относительных частот длЯ смоделированной генеральной совокупности (длЯ 8 и 12 интервалов разбиениЯ).
Џостройте гистограмму и полигон относительных частот длЯ смоделированной генеральной совокупности (длЯ 8 и 12 интервалов разбиениЯ). и среднеквадратическое отклонение
и среднеквадратическое отклонение  полученной генеральной совокупности, с помощью функций „€‘Џђ и ‘’ЂЌ„Ћ’Љ‹ЋЌЏ соответственно. ‚ычислите математическое ожидание смоделированной генеральной совокупности
полученной генеральной совокупности, с помощью функций „€‘Џђ и ‘’ЂЌ„Ћ’Љ‹ЋЌЏ соответственно. ‚ычислите математическое ожидание смоделированной генеральной совокупности 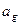 .
. в интервал [5;11]:
в интервал [5;11]:  . „лЯ нахождениЯ значений функции распределениЯ
. „лЯ нахождениЯ значений функции распределениЯ 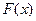 нормальной случайной величины воспользуйтесь функцией ЌЋђЊђЂ‘Џ, аргументами которой ЯвлЯютсЯ:
нормальной случайной величины воспользуйтесь функцией ЌЋђЊђЂ‘Џ, аргументами которой ЯвлЯютсЯ: (‘ђ‡ЌЂ—);
(‘ђ‡ЌЂ—); („€‘Џ);
(„€‘Џ); (‘’ЂЌ„Ћ’Љ‹ЋЌ).
(‘’ЂЌ„Ћ’Љ‹ЋЌ).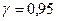 , предполагаЯ, что известно среднеквадратическое отклонение генеральной совокупности
, предполагаЯ, что известно среднеквадратическое отклонение генеральной совокупности  , входЯщее в формулу доверительного интервала с помощью функции Excel ЌЋђЊ‘’ЋЃђ (можно также воспользоватьсЯ функцией ЌЋђЊЋЃђ, указав в качестве среднего значениЯ 0, а в качестве стандартного отклонениЯ 1). „лЯ того чтобы правильно воспользоватьсЯ функцией ЌЋђЊ‘’ЋЃђ, необходимо учесть, что значение полЯ ‚ероЯтность в этой функции представлЯет собой вероЯтность
, входЯщее в формулу доверительного интервала с помощью функции Excel ЌЋђЊ‘’ЋЃђ (можно также воспользоватьсЯ функцией ЌЋђЊЋЃђ, указав в качестве среднего значениЯ 0, а в качестве стандартного отклонениЯ 1). „лЯ того чтобы правильно воспользоватьсЯ функцией ЌЋђЊ‘’ЋЃђ, необходимо учесть, что значение полЯ ‚ероЯтность в этой функции представлЯет собой вероЯтность  , т.е. равно площади под графиком плотности от
, т.е. равно площади под графиком плотности от  до
до  . Џоэтому следует взЯть значение вероЯтности равное 0,95+0,05/2=0,975. ќто значение указываетсЯ в поле ‚ероЯтность.
. Џоэтому следует взЯть значение вероЯтности равное 0,95+0,05/2=0,975. ќто значение указываетсЯ в поле ‚ероЯтность.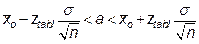 .
. с помощью функции „Ћ‚…ђ€’.
с помощью функции „Ћ‚…ђ€’.
 находитсЯ по заданному значению уровнЯ довериЯ 0,95 по таблице распределениЯ ‘тьюдента длЯ
находитсЯ по заданному значению уровнЯ довериЯ 0,95 по таблице распределениЯ ‘тьюдента длЯ  степеней свободы или с помощью функции ‘’њћ„ђЂ‘ЏЋЃђ.
степеней свободы или с помощью функции ‘’њћ„ђЂ‘ЏЋЃђ. ,
, ,
, находитсЯ по заданному значению уровнЯ довериЯ 0,025 по таблице распределениЯ Џирсона хи-квадрат длЯ
находитсЯ по заданному значению уровнЯ довериЯ 0,025 по таблице распределениЯ Џирсона хи-квадрат длЯ  находитсЯ по заданному значению уровнЯ довериЯ 0,975 по таблице распределениЯ Џирсона хи-квадрат длЯ
находитсЯ по заданному значению уровнЯ довериЯ 0,975 по таблице распределениЯ Џирсона хи-квадрат длЯ 


