Механический смысл векторного произведения
1)
 
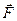 приложена к точке В. Тогда моментом силы приложена к точке В. Тогда моментом силы 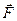 относительно точки А называется вектор относительно точки А называется вектор 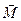 такой, что такой, что 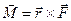 , где вектор , где вектор 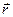 - плечо АВ, - плечо АВ, 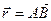 . .
2) Пусть материальная точка движется по окружности с центром в точке О,
  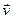 - линейная скорость движения точки, - линейная скорость движения точки,  - радиус-вектор точки М. Тогда угловой скоростью материальной точки называется вектор - радиус-вектор точки М. Тогда угловой скоростью материальной точки называется вектор 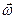 такой, что такой, что 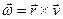 . .
Свойства векторного произведения. 1. Доказательство. Доказательство необходимости: 1) Пусть Доказательство достаточности: 1) Пусть Частный случай: 2. 3. Скалярный квадрат векторного произведения равен квадрату модуля векторного произведения: 4. Если (Пояснение: если одну из сторон параллелограмма увеличить в λ; раз, не меняя ее направление, то и площадь увеличиться в λ; раз). 5. Перемножаем, строго соблюдая порядок. 6. 7.
Таблица векторного умножения ортов
Следовательно, исходя из определения векторного произведения, можем записать, что
|





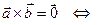
 – коллинеарные векторы. (3)
– коллинеарные векторы. (3)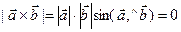 тогда и только тогда, когда
тогда и только тогда, когда  , т.е. когда
, т.е. когда  . 2) Пусть среди векторов
. 2) Пусть среди векторов  -вектор можно считать параллельным любому вектору, т.е. пусть
-вектор можно считать параллельным любому вектору, т.е. пусть  , так как
, так как  . 2) Пусть
. 2) Пусть 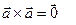
 (Пояснение: из-за смены троек)
(Пояснение: из-за смены троек) (следует из 2-го свойства скалярного произведения)
(следует из 2-го свойства скалярного произведения) – действительное число, то
– действительное число, то 
 ,
, 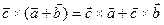

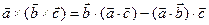
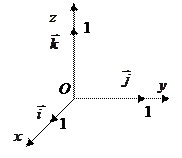 Углы
Углы  ,
,  ,
,  ,
,  ,
,  ,
, ; тогда
; тогда  ; длины ортов равны
; длины ортов равны  .
. ,
, 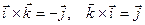 ,
,  ,
, .
.


